【ヒント掲載で使い易い】電験三種(理論)の過去問題集2019★動画と図でやさしく解説

電験三種の過去問解説(理論)：2019年(令和元年)問9
角周波数の変化した時の電流の実効値(計算)

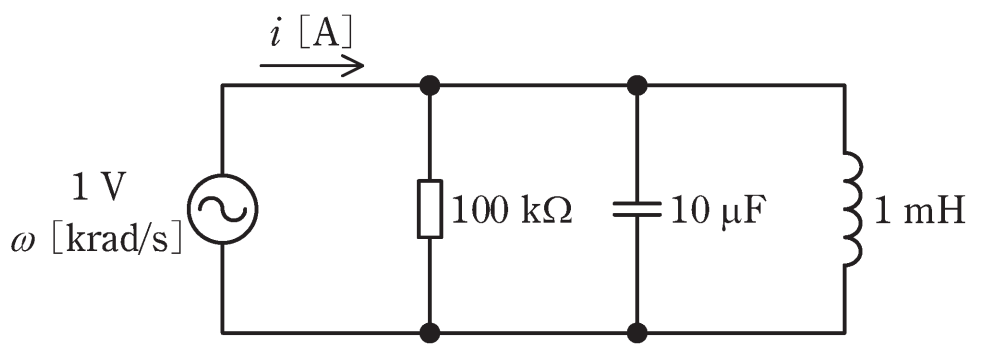
図は、実効値が1Vで角周波数ω[krad/s]が変化する正弦波交流電源を含む回路である。いま、ωの値がω₁=5krad/s、ω₂=10krad/s、ω₃=30krad/sと3通りの場合を考え、ω=ω_k(k=1,2,3)のときの電流i[A]の実効値をI_kと表すとき、I₁、I₂、I₃の大小関係として、正しいものを次の(1)～(5)のうちから一つ選べ。

\((1)I_1<I_2<I_3\)	\((2)I_1=I_2<I_3\)	\((3)I_2<I_1<I_3\)
\((4)I_2<I_1=I_3\)	\((5)I_3<I_2<I_1\)

出典元：一般財団法人電気技術者試験センター

スポンサーリンク

過去問解説

コイルとコンデンサのリアクタンスは下記式で表されます。

角周波数が変化するとリアクタンスも変化するので、3通りの角周波数ごとにリアクタンスを求めて、電流の大きさを比較しましょう。

<コンデンサのリアクタンス>
\(\displaystyle\frac{1}{jω_1C}=\displaystyle\frac{1}{j5×10^3×10×10^{-6}}\)

　　　  \(=\displaystyle\frac{1}{j0.05}\)

　　　  \(=-j20\)

<電流>
\(\dot{I_1}=\displaystyle\frac{V}{R}+\displaystyle\frac{V}{jω_1L}+\displaystyle\frac{V}{\displaystyle\frac{1}{jω_1C}}\)

　  \(=\displaystyle\frac{1}{100×10^3}+\displaystyle\frac{1}{j5}+\displaystyle\frac{1}{-j20}\)

　  \(=0.01×10^{-3}-j0.2+j0.05\)

　  \(=0.01×10^{-3}-j0.15\)

\(I_1=\sqrt{(0.01×10^{-3})^2+0.15^2}=0.15\)

<コンデンサのリアクタンス>
\(\displaystyle\frac{1}{jω_2C}=\displaystyle\frac{1}{j10×10^3×10×10^{-6}}\)

　　　  \(=\displaystyle\frac{1}{j0.1}\)

　　　  \(=-j10\)

<電流>
\(\dot{I_2}=\displaystyle\frac{1}{100×10^3}+\displaystyle\frac{1}{j10}+\displaystyle\frac{1}{-j10}\)

　  \(=0.01×10^{-3}-j0.1+j0.1\)

　  \(=0.01×10^{-3}\)

\(I_2=\sqrt{(0.01×10^{-3})^2}=0.01×10^{-3}\)

<コンデンサのリアクタンス>
\(\displaystyle\frac{1}{jω_3C}=\displaystyle\frac{1}{j30×10^3×10×10^{-6}}\)

　　　  \(=\displaystyle\frac{1}{j0.3}\)

　　　  \(=-j\displaystyle\frac{10}{3}\)

<電流>
\(\dot{I_3}=\displaystyle\frac{1}{100×10^3}+\displaystyle\frac{1}{j30}+\displaystyle\frac{1}{-j\displaystyle\frac{10}{3}}\)

　  \(=0.01×10^{-3}-j0.033+j0.3\)

　  \(=0.01×10^{-3}+j0.267\)

\(I_3=\sqrt{(0.01×10^{-3})^2+0.267^2}=0.267\)

したがって、(3)が正解です。