電験三種の過去問解説(理論):2019年(令和元年)問16
三相交流における電源電流と負荷の有効電力(計算)
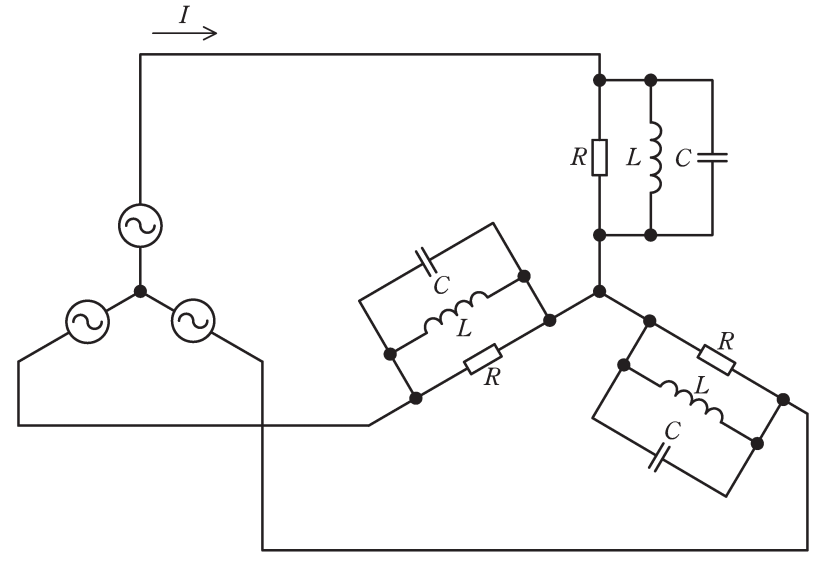
図のように線間電圧200V、周波数50Hzの対称三相交流電源
にRLC負荷が接続されている。R=10Ω、電源角周波数をω[ rad/s]として、ωL=10Ω、\(\displaystyle\frac{1}{ωC}=20Ω\)である。 次の(a)及び(b)の問に答えよ。
(a)電源電流Iの値[A]
として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)7 (2)10 (3)13 (4)17 (5)22
(b)三相負荷の有効電力の値[kW]として、 最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)1.3 (2)2.6 (3)3.6 (4)4.0 (5)12
スポンサーリンク
過去問解説
(a)電源電流の値
三相回路の計算問題では、一相に着目して解きます。
『相電圧』と『交流計算する場合のリアクタンス』が、下記式のようになることを用いて、一相あたりの等価回路を描いてみましょう。
相電圧
\(E=\displaystyle\frac{V}{\sqrt3}[V]\)
リアクタンス
・コイル \(jX_L=jωL\)
・コンデンサ \(-jX_C=\displaystyle\frac{1}{jωC}\)
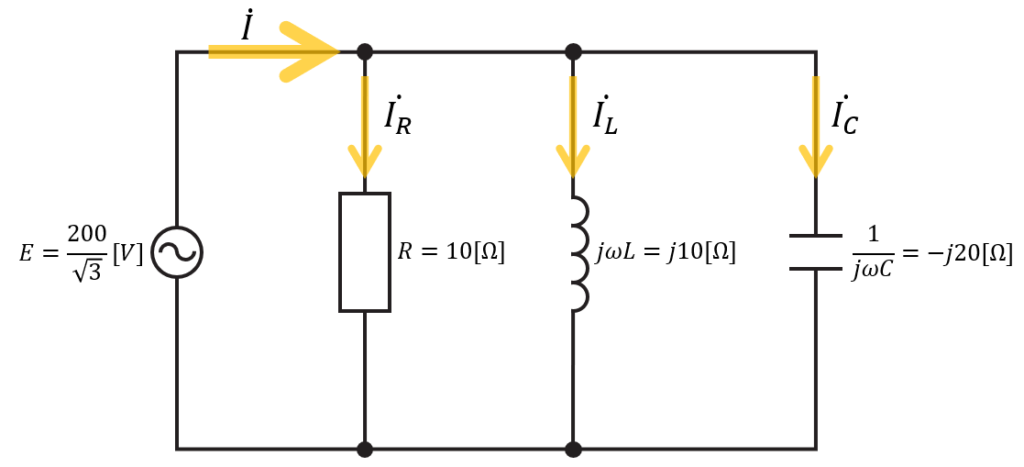
電源電流\(\dot{I}\)は、抵抗・コイル・コンデンサを流れる電流の合計となるため、
\(\dot{I}=\dot{I_R}+\dot{I_L}+\dot{I_C}\)
\(=\displaystyle\frac{E}{R}+\displaystyle\frac{E}{jωL}+\displaystyle\frac{E}{\displaystyle\frac{1}{jωC}}\)
\(=E(\displaystyle\frac{1}{R}+\displaystyle\frac{1}{jωL}+\displaystyle\frac{1}{\displaystyle\frac{1}{jωC}})\)
\(=\displaystyle\frac{200}{\sqrt3}(\displaystyle\frac{1}{10}+\displaystyle\frac{1}{j10}+\displaystyle\frac{1}{-j20})\)
\(=\displaystyle\frac{200}{\sqrt3}(\displaystyle\frac{1}{10}-j\displaystyle\frac{1}{10}+j\displaystyle\frac{1}{20})\)
\(=\displaystyle\frac{200}{\sqrt3}(\displaystyle\frac{1}{10}-j\displaystyle\frac{1}{20})\)
\(=\displaystyle\frac{20}{\sqrt3}-j\displaystyle\frac{10}{\sqrt3}\)
よって、\(\dot{I}\)の大きさは、
\(I=\sqrt{(\displaystyle\frac{20}{\sqrt3})^2+(\displaystyle\frac{10}{\sqrt3})^2}\)
\(=\sqrt{\displaystyle\frac{400}{3}+\displaystyle\frac{100}{3}}\)
\(=\sqrt{\displaystyle\frac{500}{3}}\)
\(=12.9[A]\)
したがって。最も近い(3)が正解です。
(b)三相負荷の有効電力の値
三相負荷の有効電力は、一相あたりの有効電力を3倍すれば求められます。
有効電力
・一相当たり \(P_1=\displaystyle\frac{E^2}{R}\)
・三相負荷 \(P_3=3P_1\)
\(P_1=\displaystyle\frac{(\displaystyle\frac{200}{\sqrt3})^2}{10}\)
\(=\displaystyle\frac{\displaystyle\frac{40000}{3}}{10}\)
\(=\displaystyle\frac{4000}{3}[W]\)
となるので、
\(P_3=3P_1\)
\(=3×\displaystyle\frac{4000}{3}\)
\(=4000[W]\)
\(=4[kW]\)
したがって、(4)が正解です。