【ヒント掲載で使い易い】電験三種(理論)の過去問題集2019★動画と図でやさしく解説

電験三種の過去問解説(理論)：2019年(令和元年)問10
時定数と抵抗で消費されるエネルギー(計算)

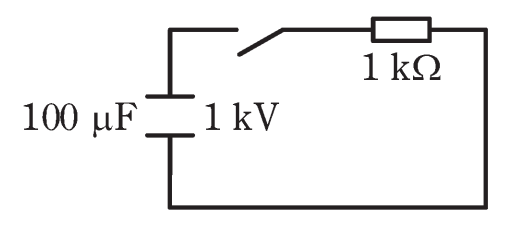
図のように、電圧1kVに充電された静電容量100μFのコンデンサ、抵抗1kΩ、スイッチからなる回路がある。スイッチを閉じた直後に過渡的に流れる電流の時定数τの値[s]と、スイッチを閉じてから十分に時間が経過するまでに抵抗で消費されるエネルギーWの値[J]の組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

	τ	W
(1)	0.1	0.1
(2)	0.1	50
(3)	0.1	1000
(4)	10	0.1
(5)	10	50

出典元：一般財団法人電気技術者試験センター

スポンサーリンク

過去問解説

時定数は過渡現象が生じる速さを表す指標になり、下記式で求められます。

問題文より、静電容量100μF、抵抗1kΩが与えられているので、単位に注意して式に代入しましょう。

\(τ=100×10^{-6}×1×10^3=0.1[s]\)

次に、スイッチを閉じてから十分に時間が経過するまでに抵抗で消費されるエネルギーですが、

コンデンサに蓄えられていたエネルギーと等しくなります。

問題文より、電圧1kV、静電容量100μFが与えられているので、単位に注意して式に代入しましょう。

\(P=\displaystyle\frac{1}{2}×100×10^{-6}×(1×10^3)^2\)

　 \(=50[J]\)

したがって、(2)が正解です。