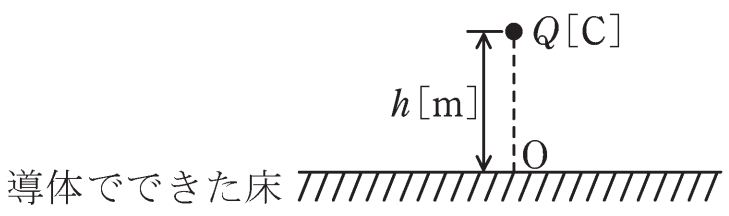電験三種の過去問解説(理論):2019年(令和元年)問15
電気力線の様子と鉛直方向に引き上げる仕事(計算)
図のように、平らで十分大きい導体でできた床から高さh[m]の
位置に正の電気量Q[C]をもつ点電荷がある。次の(a)及び( b)の問に答えよ。ただし、点電荷から床に下ろした垂線の足を点 O、床より上側の空間は真空とし、床の導体は接地されている。真 空の誘電率をε0[F/m]とする。
(a)床より上側の電界は、
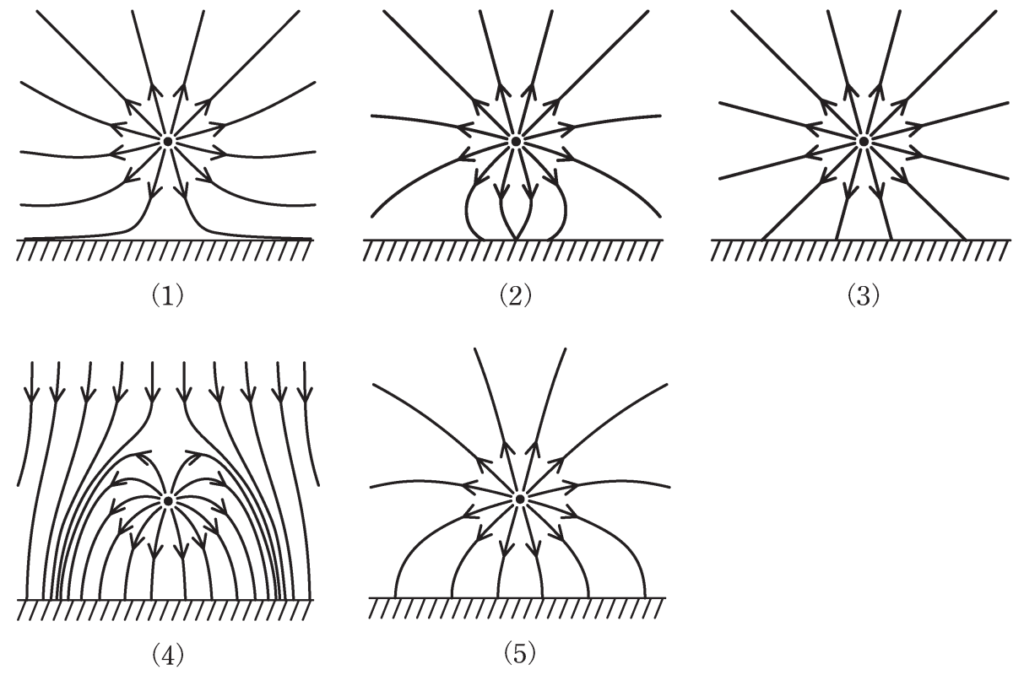
点電荷をつくる電界と、床の表面に静電誘導によって現れた面電荷 のつくる電界との和になる。床より上側の電気力線の様子として、 適切なものを次の(1)~(5)のうちから一つ選べ。
(b)点電
荷は床表面に現れた面電荷から鉛直方向の静電吸引力F[N]を受 ける。その力は床のない状態で点Oに固定した電気量\(-\displaystyle\frac{Q}{4}[C]\)の点電荷から受ける静電力に等しい。F[N]に逆らって、 点電荷を高さh[m]からz[m](ただしh<z)まで鉛直方向 に引き上げるのに必要な仕事W[J]を表す式として、 正しいものを次の(1)~(5)のうちから一つ選べ。
\((1)\displaystyle\frac{Q^2}{4πε_0z^2}\) \((2)\displaystyle\frac{Q^2}{4πε_0}(\displaystyle\frac{1}{h}-\displaystyle\frac{1}{z})\) \((3)\displaystyle\frac{Q^2}{16πε_0}(\displaystyle\frac{1}{h}-\displaystyle\frac{1}{z})\) \((4)\displaystyle\frac{Q^2}{16πε_0z^2}\) \((5)\displaystyle\frac{Q^2}{πε_0}(\displaystyle\frac{1}{h^2}-\displaystyle\frac{1}{z^2})\)
スポンサーリンク
過去問解説
(a)電気力線の様子
電気力線のポイントは下記の通りである。
電気力線
・正の電荷から負の電荷へ入る
・電気力線同士は交わらない
・等電位面(導体の表面など)に直交する
(1)は、電気力線が『正の電荷から負の電荷に入っていない』ので誤り。
(2)は、電気力線が『交わっており、かつ等電位面に直交していない』ので誤り。
(3)は、電気力線が『直交していない』ので誤り。
(4)は、電気力線が『正の電荷以外から負の電荷に入っている』ので誤り。
したがって、全てのポイントを満たす(5)が正解です。
(b)電荷を鉛直方向に引き上げるの必要な仕事
\(Q[C]\)と\(-\displaystyle\frac{Q}{4}[C]\)で符号の異なる電荷において、お互いが引き寄せあう方向に吸引力が働く。
電荷の吸引力
\(F=\displaystyle\frac{Q_1Q_2}{4πε_0h^2}\)
上記式を参考に、h点の吸引力とz点の吸引力を表す式は、
\(F_h=\displaystyle\frac{Q×\displaystyle\frac{Q}{4}}{4πε_0h^2}=\displaystyle\frac{Q^2}{16πε_0h^2}\)
\(F_z=\displaystyle\frac{Q×\displaystyle\frac{Q}{4}}{4πε_0z^2}=\displaystyle\frac{Q^2}{16πε_0z^2}\)
となる。
吸引力に逆らって鉛直方向に引き上げるのに必要な仕事は、『力×距離』で求められるので、h点のエネルギーとz点のエネルギーを表す式は、
\(W_h=\displaystyle\frac{Q^2}{16πε_0h^2}×h=\displaystyle\frac{Q^2}{16πε_0h}\)
\(W_z=\displaystyle\frac{Q^2}{16πε_0z^2}×h=\displaystyle\frac{Q^2}{16πε_0z}\)
となる。
よって、h点からz点まで引き上げるのに必要な仕事は、
\(W=W_h-W_z\)
\(=\displaystyle\frac{Q^2}{16πε_0h}-\displaystyle\frac{Q^2}{16πε_0z}\)
\(=\displaystyle\frac{Q^2}{16πε_0}(\displaystyle\frac{1}{h}-\displaystyle\frac{1}{z})\)
したがって、(3)が正解です。