令和2年度(2020年):第三種電気主任技術者試験(理論)問3
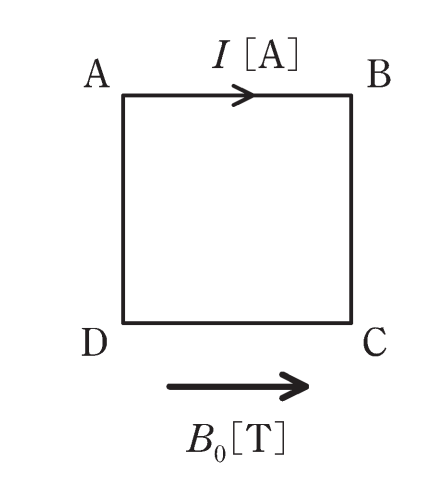
平等な磁束密度\(B_0[T]\)のもとで、一辺の長さが\(h[m]\)の正方形ループABCDに直流電流\(I[A]\)が流れている。\(B_0[T]\)の向きは辺ABと平行である。\(B_0[T]\)がループに及ぼす電磁力として、正しいものを次の(1)~(5)のうちから一つ選べ。
(1)大きさ\(2IhB_0[N]\)の力
(2)大きさ\(4IhB_0[N]\)の力
(3)大きさ\(Ih^2B_0[N・m]\)の偶力のモーメント
(4)大きさ\(2Ih^2B_0[N・m]\)の偶力のモーメント
(5)力も偶力のモーメントも働かない
動画解説
過去問解説(2020年理論問3)
平等な磁束密度\(B_0[T]\)のもとで導体に電流を流すと、フレミング左手の法則に従った方向に電磁力が生じます。
電磁力は、磁束と電流の向きが直交している場合に働くので、辺BCと辺ADに生じます。
フレミング左手の法則より、
辺BC:上向きの電磁力
辺AD:下向きの電磁力
が生じます。
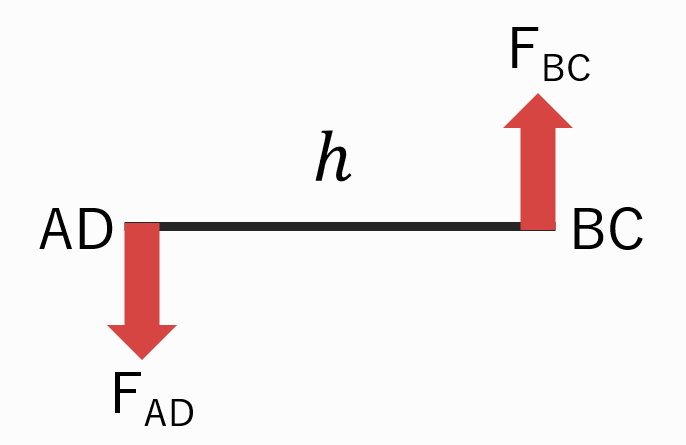
電磁力は下記公式で求められるので、
電磁力の公式
\(F=ILB[N]\)
\(I:電流[A]\)
\(L:導体の長さ[m]\)
\(B:磁束密度[T]\)
辺BCと辺ADに働く電磁力は、
\(F_{BC}=IhB_0[N]\)
\(F_{AD}=IhB_0[N]\)
と表せる。
この時、電磁力の作用点が異なるので、力の足し算や引き算はできません。
辺BCに上向きの電磁力…辺ADに下向きの電磁力が生じるので、正方形ループABCDには反時計回りに回転する力のモーメントが生じます。
(*同じ大きさで平行かつ反対向きの力を偶力と言います)
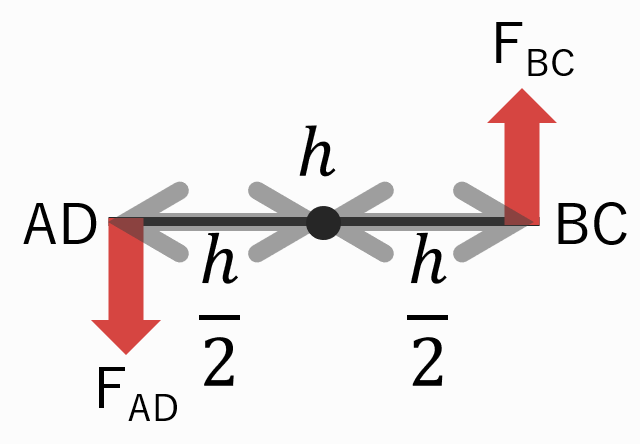
力のモーメントは下記式で求められるので、
力のモーメント
\(M=Fr[N・m]\)
\(F:力[N]\)
\(r:回転軸から作用点までの距離[m]\)
辺BCと辺ADに生じる力のモーメントは、
\(M_{BC}=F_{BC}×\displaystyle\frac{h}{2}\)
\(=IhB_0×\displaystyle\frac{h}{2}\)
\(=\displaystyle\frac{Ih^2B_0}{2}\)
\(M_{AD}=F_{BC}×\displaystyle\frac{h}{2}\)
\(=IhB_0×\displaystyle\frac{h}{2}\)
\(=\displaystyle\frac{Ih^2B_0}{2}\)
\(M_{BC}=M_{AD}\)となり、偶力によるモーメントの和より、
\(M=M_{BC}+M_{AD}\)
\(=\displaystyle\frac{Ih^2B_0}{2}+\displaystyle\frac{Ih^2B_0}{2}\)
\(=Ih^2B_0[N・m]\)
従って、(3)が正解です。