令和2年度(2020年):第三種電気主任技術者試験(理論)問10
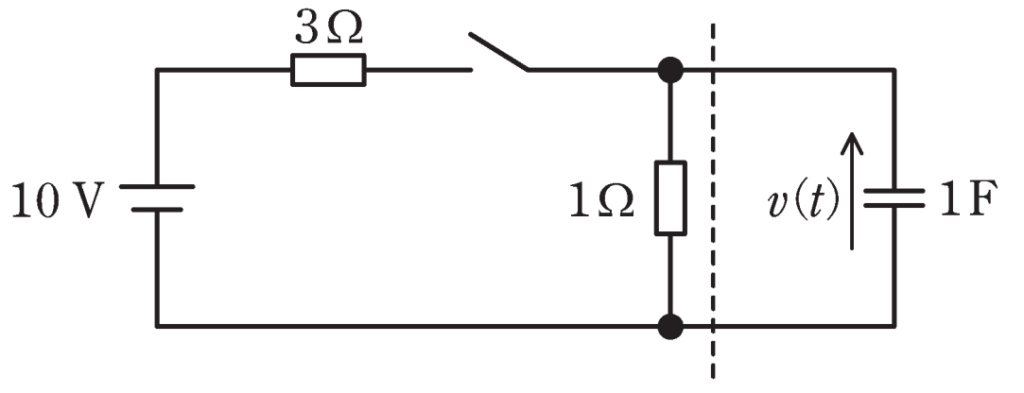
図の回路のスイッチを閉じたあとの電圧v(t)の波形を考える。破線から左側にテブナンの定理を適用することで、回路の時定数[s]とv(t)の最終地[V]の組合せとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、初めスイッチは開いており、回路は定常状態にあったとする。
時定数[s] 最終値[V] (1) 0.75 10 (2) 0.75 2.5 (3) 4 2.5 (4) 1 10 (5) 1 0
動画解説
過去問の解説(2020年理論問10)
回路の時定数と電圧を求める計算問題ですが、問題文にしたがってテブナンの定理が使えれば解けます。
テブナンの定理は、
・開放端起電力
・合成抵抗
を求めるので、まずは開放端起電力\(V_{ab}\)を求めていきましょう。
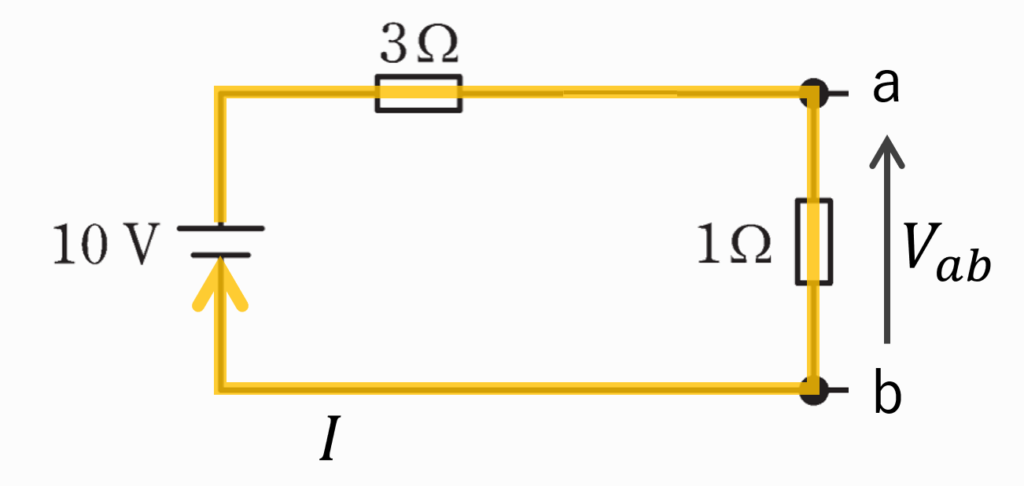
回路を流れる電流\(I\)はオームの法則より、
\(I=\displaystyle\frac{10}{3+1}=2.5[A]\)
となるので、開放端起電力\(V_{ab}\)は、
\(V_{ab}=1×2.5=2.5[V]\)
となります。
次に、a-b端子から見た合成抵抗は、
\(R=\displaystyle\frac{3×1}{3+1}=0.75[Ω]\)
となります。
従って、問題図の回路は
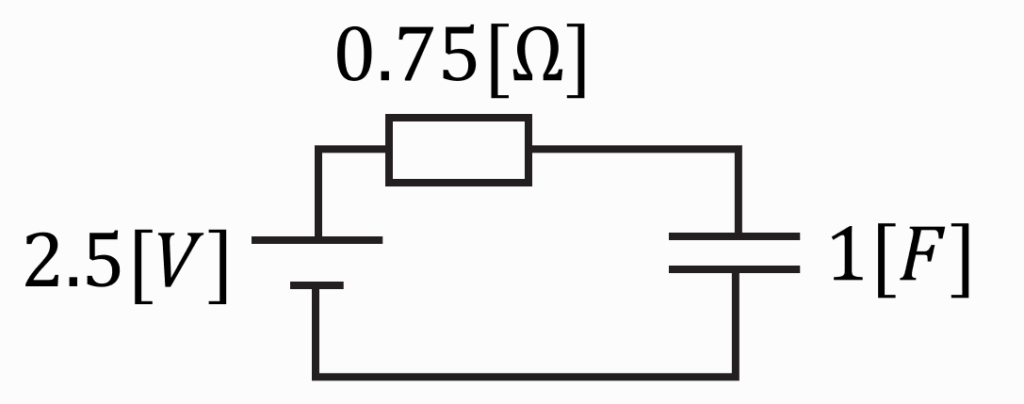
このように変換することができ、時定数は
回路の時定数
\(T=RC\)
で求められるので、
\(T=0.75×1=0.75[s]\)
となります。
また、コンデンサの電圧v(t)は最終的に\(V_{ab}\)と等しくなるので、2.5[V]となります。
よって、(2)が正解です。