【ヒント掲載で使い易い】電験三種(機械)の過去問題集2019★動画と図でやさしく解説

電験三種の過去問解説(機械)：2019年(令和元年)問11
エレベータの上昇速度(計算)

かごの質量が250kg、定格積載質量が1500kgのロープ式エレベータにおいて、釣合いおもりの質量は、かごの質量に定格積載質量の50%を加えた値とした。このエレベータの電動機出力を22kWとした場合、一定速度でかごが上昇しているときの速度の値[m/min]はいくらになるか、最も近いものを次の(1)～(5)のうちから一つ選べ。ただし、エレベータの機械効率は70%、積載量は定格積載質量とし、ロープの質量は無視するものとする。

(1)54

(2)94

(3)126

(4)180

(5)377

出典元：一般財団法人電気技術者試験センター

スポンサーリンク

過去問解説

先ずは、エレベータの状態を簡単な図にしておきましょう。

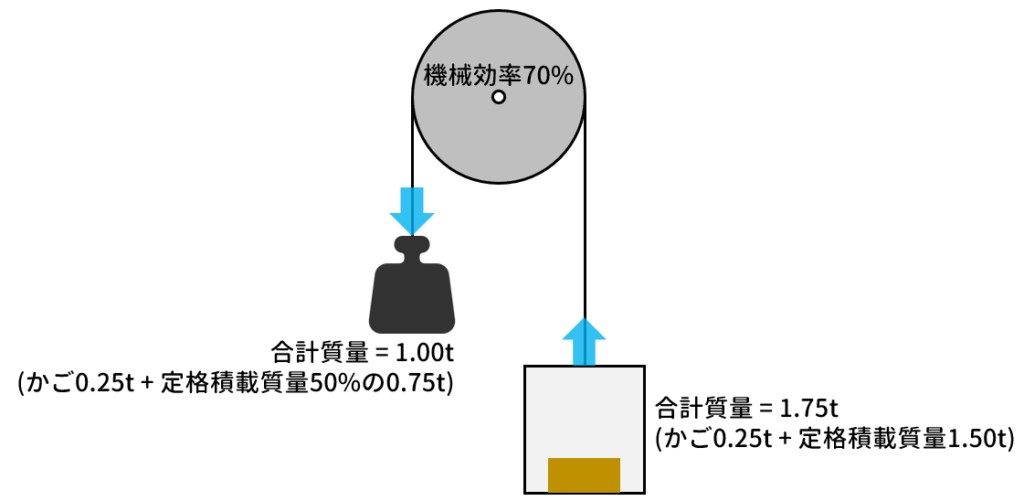
そして、上昇速度はエレベータの電動機出力(下記式)を利用して求めます。

持ち上げる質量Wは、『エレベータの質量 - 釣合いおもりの質量』で求められるので、

\(W=(0.25+1.5)-(0.25+1.5×0.5)\)

　  \(=1.75-1\)

　  \(=0.75[t]\)

となります。

エレベータの電動機出力の式から、上昇速度を求めましょう。

\(P=\displaystyle\frac{Wv}{6.12η}\)

 \(v=\displaystyle\frac{6.12ηP}{W}\)

　 \(=\displaystyle\frac{6.12×0.7×22}{0.75}\)

　 \(=126[m/min]\)

したがって、(3)が正解です。