電験三種の過去問解説(機械):2019年(令和元年)問5
同期電動機の入出力とトルク(穴埋)
次の文章は、星形結線の円筒形三相同期電動機の入力、出力、トル
クに関する記述である。
この三相同期電動機の1相分の誘導起電力
E[V]、電圧V[V]、電流I[A]、VとIの位相差をθ[ rad]としたときの1相分の入力Pi[W]は次式で表される。
\(P_i=VIcosθ\) また、EとVの位相差をδ[rad]
とすると、1相分の出力Po[W]は次式で表される。 EとVの位相差δは \(\fbox{ (ア) }\) といわれる。 \(P_o=EIcos(δ-θ)=\displaystyle\frac{VE}{x} \fbox{ (イ) }\)
ここでx[Ω]は同期リアクタンスであり、電機子巻線抵抗は無視
できるものとする。 この三相同期電動機の全出力をP[W]、
同期速度をns[min-1]とすると、トルクT[N・m]と Pの関係は次式で表される。 \(P=3P_o=2π\displaystyle\frac{n_s}{60}T\)
これか
ら、Tは次式のようになる。 \(T=\displaystyle\frac{60}{2πn_s}・3P_o=\displaystyle\frac{60}{2πn_s}・\displaystyle\frac{3VE}{x} \fbox{ イ }\)
以上のことから、\(0≦δ≦\displaystyle\frac{π}{2}\)の範囲においてδが\(\fbox{ (ウ) }\) なるに従ってTは \(\fbox{ (エ) }\) なり、理論上\(\displaystyle\frac{π}{2}\)[rad]のとき \(\fbox{ (オ) }\) となる。
上記の記述中の空白箇所(ア)、(イ)、(ウ)、(エ)
及び(オ)に当てはまる組合せとして、正しいものを次の(1)~ (5)のうちから一つ選べ。
(ア) (イ) (ウ) (エ) (オ) (1) 負荷角 cosδ 大きく 大きく 最大値 (2) 力率角 cosδ 大きく 小さく 最小値 (3) 力率角 sinδ 小さく 小さく 最小値 (4) 負荷角 sinδ 大きく 大きく 最大値 (5) 負荷角 cosδ 小さく 小さく 最大値
スポンサーリンク
過去問解説
(ア):負荷角
誘導起電力Eと電圧Vの位相差δを負荷角と言います。
(イ):sinδ
1相分の同期電動機の出力は
\(P_o=\displaystyle\frac{VE}{x}sinδ\)
となります。
ちなみに、全出力(3相分)は\(P=3P_o\)となります。
1相分、3相分の出力を求める式は暗記しておきましょう。
(ウ):大きく
(エ):大きく
(オ):最大値
トルクTと全出力Pの関係は
\(P=ωT=2πfT=2π\displaystyle\frac{n_s}{60}T\)
で表せることから、トルクは次式のようになる。
\(T=\displaystyle\frac{60}{2πn_s}P\)
\(=\displaystyle\frac{60}{2πn_s}・\displaystyle\frac{3VE}{x}・sinδ\)
sinカーブは下記のように、\(δ=\displaystyle\frac{π}{2}\)のとき最大値となる。
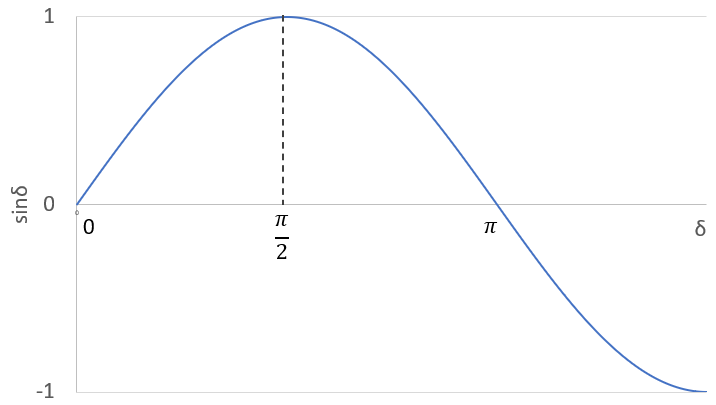
また、sinカーブを見てわかる通り、\(0≦δ≦\displaystyle\frac{π}{2}\)の範囲において、
δが大きくなるに従ってTは大きくなり、δが小さくなるにしたがってTは小さくなります…
つまり(ウ)(エ)はどちらも正しいので、(ア)(イ)(オ)より(4)が正解です。
