【使いやすさNo.1】電験三種(電力)の過去問解説集2018★動画と図でやさしく説明

電験三種の過去問解説(電力)：2018年(平成30)問17
パーセント法で示した送電線路のリアクタンスと送電電力(計算)

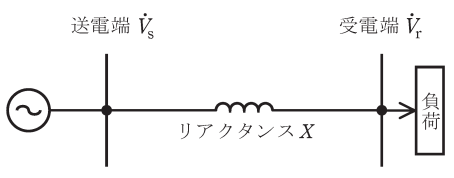
図のように、抵抗を無視できる一回線短距離送電線路のリアクタンスと送電電力について、次の(a)及び(b)の問に答えよ。ただし、一相分のリアクタンス\(X=11Ω\)、受電端電圧\(V_r\)は\(66kV\)で常に一定とする。

(a)基準容量を\(100MV・A\)、基準電圧を受電端電圧\(V_r\)としたときの送電線路のリアクタンスをパーセント法で示した値[%]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1)0.4

(2)2.5

(3)25

(4)40

(5)400

(b)送電電圧\(V_s\)を\(66kV\)、相差角(送電端電圧\(\dot{V}_s\)と受電端電圧\(\dot{V}_r\)の位相差)\(\delta\)を\(30°\)としたとき、送電電力\(P_s\)の値\([MW]\)として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1)22

(2)40

(3)198

(4)343

(5)3960

出典元：一般財団法人電気技術者試験センター

スポンサーリンク

過去問のポイント

パーセントインピーダンスは知っているけど、パーセントリアクタンスは知らなくて解けなかった方もいらっしゃるかもしれません。

今回は問題文中に『抵抗を無視できる』と記載されているため、『パーセントインピーダンス=パーセントリアクタンス』と解釈することができます。

あとは、公式に代入するだけなので、混乱しなかった方には簡単なサービス問題でしたね。

(a)パーセント法で示した送電線のリアクタンス

『抵抗を無視できる』と記載されているため、『パーセントインピーダンス=パーセントリアクタンス』と解釈して計算しましょう。

\(\%X=\displaystyle\frac{\sqrt3IX}{V_r}×100[\%]\)

分母と分子に\(V_r\)をかけます

\(\%X=\displaystyle\frac{\sqrt3V_rIX}{V_r^2}×100[\%]\)

\(\%X=\displaystyle\frac{SX}{V_r^2}×100[\%]\)

　　 \(=\displaystyle\frac{100×10^6×11}{(66×10^3)^2}×100\)

　　 \(=25.25[\%]\)

したがって、(3)が正解です。

スポンサーリンク

(b)送電電力

送電電力の公式に各数値を代入しましょう。

\(P_s=\displaystyle\frac{66×10^3×66×10^3}{11}×\displaystyle\frac{1}{2}\)

　  \(=198,000,000[W]\)

　  \(=198[MW]\)

したがって、(3)が正解です。