電験三種の過去問解説(電力)：2017年(平成29)問17
力率改善用コンデンサの総容量とパーセントインピーダンスの値(計算)
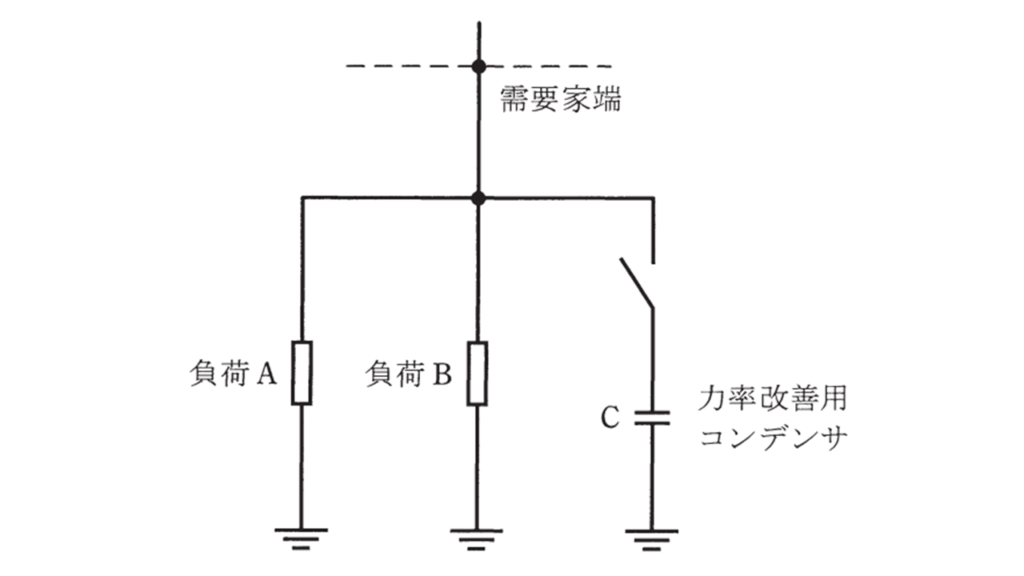
特別高圧三相3線式専用1回線で、6000kW(遅れ力率90%)の負荷Aと3000kW(遅れ力率95%)の負荷Bに受電している需要家がある。次の(a)及び(b)の問に答えよ。
(a)需要家全体の合成力率を100%にするために必要な力率改善用コンデンサの総容量の値[kvar]として、最も近いものを次の(1)～(5)のうちから一つ選べ。
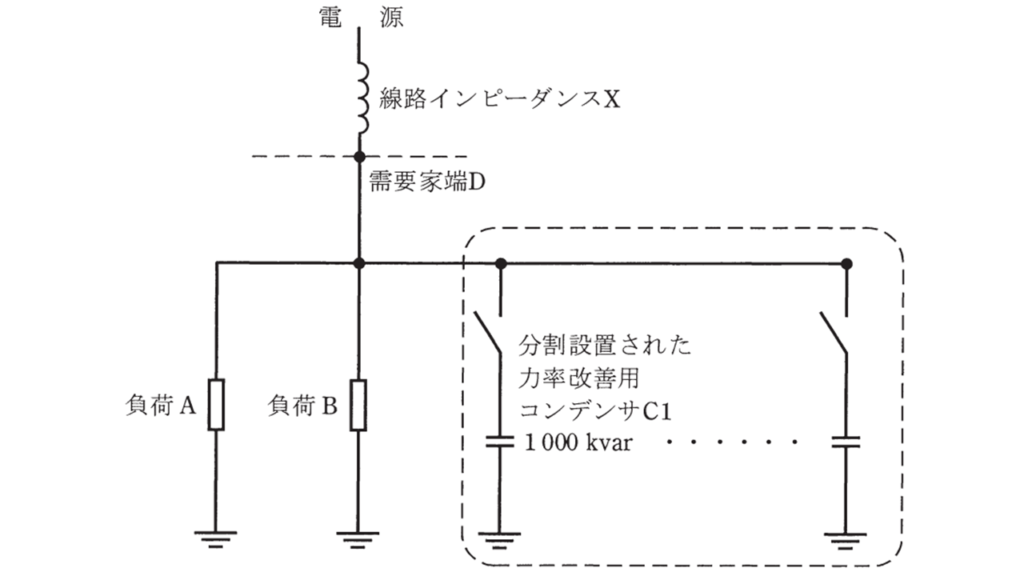
(1)1430 (2)2900 (3)3550 (4)3900 (5)4360 (b)力率改善用コンデンサの投入・開放による電圧変動を一定値に抑えるために力率改善用コンデンサを分割して設置・運用する。下図のように分割設置する力率改善用コンデンサのうち1台(C1)は容量が1000kvarである。C1を投入したとき、投入前後の需要家端Dの電圧変動率が0.8%であった。需要家端Dから電源側を見たパーセントインピーダンスの値[%](10MV・Aベース)として、最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし、線路インピーダンスXはリアクタンスのみとする。また、需要家構内の線路インピーダンスは無視する。
(1)1.25 (2)8.00 (3)10.0 (4)12.5 (5)15.0 出典元：一般財団法人電気技術者試験センター
+ ヒントを見る
<電力の三角形>
パーセントインピーダンスの公式
\(\%Z=\displaystyle\frac{ZI}{E}×100[\%]\)
電圧変動率の公式
\(ε=\displaystyle\frac{ΔV}{V}×100[\%]\)
スポンサーリンク
過去問のポイント
電力の三角形、パーセントインピーダンスの公式、電圧変動率の公式…これらを覚えていることが大切な問題です。
(a)力率改善用コンデンサの総容量
力率改善用コンデンサの総容量の値は、負荷Aと負荷Bの無効電力を足し算して求められます。
step
1負荷AとBの無効電力
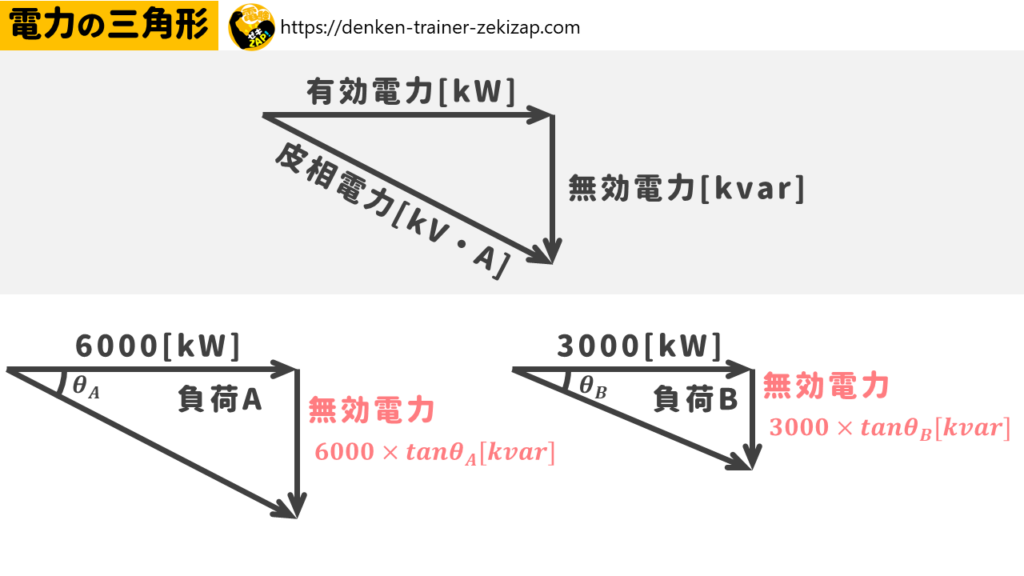
電力の三角形を参考に、負荷Aと負荷Bの無効電力を求めてみましょう。
\(負荷Aの無効電力=6000×tanθ_A\)
\(=6000×\displaystyle\frac{sinθ_A}{cosθ_A}\)
\(=6000×\displaystyle\frac{\sqrt{1-cos^2θ_A}}{cosθ_A}\)
\(=6000×\displaystyle\frac{\sqrt{1-0.9^2}}{0.9}\)
\(=6000×0.4843\)
\(=2906[kvar]\)
\(負荷Bの無効電力=3000×tanθ_B\)
\(=3000×\displaystyle\frac{sinθ_B}{cosθ_B}\)
\(=3000×\displaystyle\frac{\sqrt{1-cos^2θ_B}}{cosθ_B}\)
\(=3000×\displaystyle\frac{\sqrt{1-0.95^2}}{0.95}\)
\(=3000×0.3287\)
\(=986[kvar]\)
step
2力率改善用コンデンサの総容量
負荷Aと負荷Bの無効電力を足し算して需要家全体の無効電力を求めましょう。
\(2906+986=3892[kvar]\)
需要家全体の合成力率を100%にするとは、需要家全体の無効電力をゼロにするということなので、3892[kvar]の力率改善用コンデンサを接続すれば良いということになります。
したがって、一番近い値である(4)3900[kvar]が正解です。
(b)需要家端Dから電源側を見たパーセントインピーダンス
パーセントインピーダンスの公式
\(\%Z=\displaystyle\frac{ZI}{E}×100[\%]\)
電圧変動率の公式
\(ε=\displaystyle\frac{ΔV}{V}×100[\%]\)
パーセントインピーダンスの公式と電圧変動率の公式を、1000kvarと10MV・Aを含む形に変換しましょう。
step
1パーセントインピーダンスの公式
\(\%Z=\displaystyle\frac{ZI}{E}×100[\%]\)
\(\%Z=\displaystyle\frac{ZI}{\displaystyle\frac{V}{\sqrt3}}×100[\%]\)
\(\%Z=\displaystyle\frac{\sqrt3ZI}{V}×100[\%]\)
\(\%Z=\displaystyle\frac{\sqrt3VIZ}{V^2}×100[\%]\)
\(\%Z=\displaystyle\frac{PZ}{V^2}×100[\%]\)
今回の問題では\(Z=X\)なので、
\(\%Z=\displaystyle\frac{PX}{V^2}×100[\%]\)
step
2電圧変動率の公式
\(ε=\displaystyle\frac{ΔV}{V}×100[\%]\)
\(ε=\displaystyle\frac{\sqrt3I(Rcosθ+Xsinθ)}{V}×100[\%]\)
\(ε=\displaystyle\frac{\sqrt3IXsinθ}{V}×100[\%]\)
\(ε=\displaystyle\frac{\sqrt3VIXsinθ}{V^2}×100[\%]\)
\(ε=\displaystyle\frac{QX}{V^2}×100[\%]\)
step
3需要家端Dから電源側を見たパーセントインピーダンス
パーセントインピーダンスと電圧変動率を比の関係で整理してみましょう。
\(\%Z:ε=\displaystyle\frac{PX}{V^2}×100:\displaystyle\frac{QX}{V^2}×100\)
\(\%Z:ε=P:Q\)
\(\%Z×Q=ε×P\)
\(\%Z=\displaystyle\frac{ε×P}{Q}=\displaystyle\frac{0.8×10×10^6}{1000×10^3}\)
\(\%Z=8[\%]\)
したがって、(2)が正解です。