電験三種の過去問解説(電力):2017年(平成29)問8
電線最低点における水平張力(計算)
支持点間が180m、たるみが3.0mの架空電線路がある。
いま架空電線路の支持点間を200mにしたとき、たるみを4.0mにしたい。電線の最低点における水平張力をもとの何[%]にすればよいか。最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、支持点間の高低差はなく、電線の単位長当たりの荷重は変わらないものとし、その他の条件は無視するものとする。
(1)83.3 (2)92.6 (3)108.0 (4)120.0 (5)148.1
スポンサーリンク
過去問のポイント
電線のたるみの公式を利用した計算問題です。
公式を覚えていることが前提になりますが、覚えていれば簡単だったと思います。
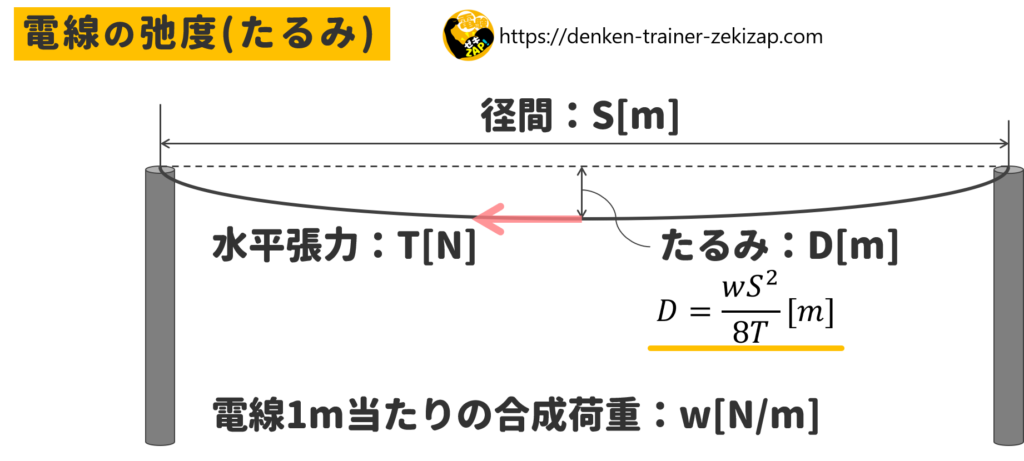
たるみの公式
\(D=\displaystyle\frac{wS^2}{8T}[m]\)
\(T=\displaystyle\frac{wS^2}{8D}[N]\)
たるみが3[m]の時の水平張力\(T_1\)、たるみが4[m]の時の水平張力\(T_2\)として、
電線の最低点における水平張力をもとの何[%]にすればよいかを求めましょう。
\(\displaystyle\frac{T_2}{T_1}=\frac{\displaystyle\frac{w×200^2}{8×4}}{\displaystyle\frac{w×180^2}{8×3}}×100[\%]\)
\(=\frac{\displaystyle\frac{200^2}{4}}{\displaystyle\frac{180^2}{3}}×100[\%]\)
\(=\displaystyle\frac{10000}{10800}×100[\%]\)
\(=92.6[\%]\)
したがって、(2)が正解です。
