電験三種の過去問解説(電力):2017年(平成29)問11
三相4線式の線路損失は単相2線式の何%(計算)
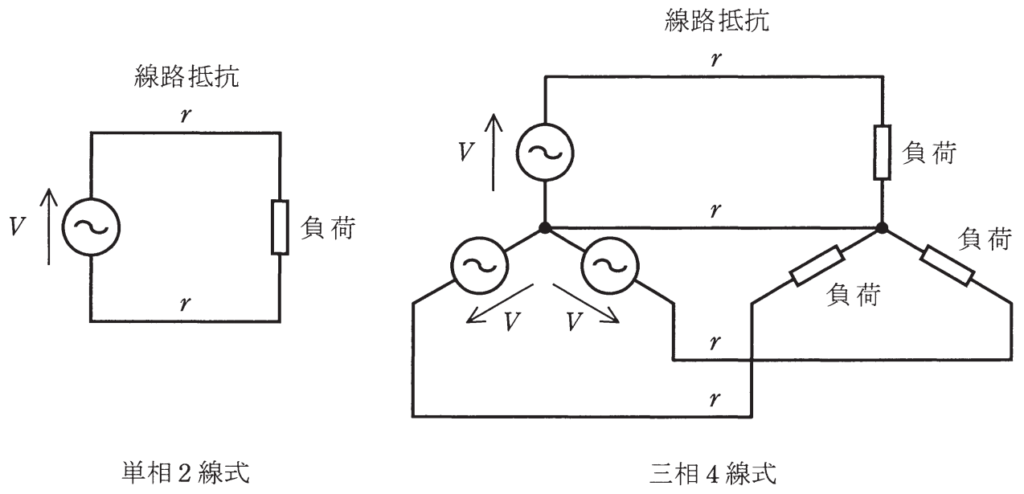
回路図のような単相2線式及び三相4線式のそれぞれの低圧配電方式で、抵抗負荷に送電したところ送電電力が等しかった。
このときの三相4線式の線路損失は単相2線式の何[%]となるか、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、三相4線式の結線はY結線で、電源は三相対称、負荷は三相平衡であり、それぞれの低圧配電方式の1線当たりの線路抵抗r、回路図に示す電圧Vは等しいものとする。また、線路インダクタンスは無視できるものとする。
(1)16.7 (2)33.3 (3)50.0 (4)57.8 (5)66.7
スポンサーリンク
過去問のポイント
単相2線式と三相4線式の『送電電力』と『線路損失』の公式を覚えていないと解けない計算問題です。
図に示されている三相4線式の電圧Vが、相電圧であることに注意して公式を使用しましょう!
(*相電圧はVではなくEで勉強されている方も多いと思いますが…今回の問題は相電圧をVとしています。…表記が違うだけですが、私は試験本番で間違えました(--,))
求め方
三相4線式の線路損失は単相2線式の何[%]となるか?
\(\displaystyle\frac{P_{3L}}{P_{1L}}×100[\%]\)
上記の式から求められます。
『三相4線式の線路損失の公式』と『単相2線式の線路損失の公式』をそれぞれ変換しましょう。
線路損失の公式
<単相2線式>
\(P_{1L}=2rI_1^2\)
<三相4線式>
\(P_{3L}=3RI_3^2\)
\(\displaystyle\frac{P_{3L}}{P_{1L}}×100[\%]=\displaystyle\frac{3rI_3^2}{2rI_1^2}×100[\%]\)
\(=\displaystyle\frac{3I_3^2}{2I_1^2}×100[\%]\)
分母に\(I_1\)、分子に\(I_3\)があり、打ち消せないため、送電電力の公式を変換して代入してみましょう♪
送電電力の公式
<単相2線式>
\(P=VI_1cosθ\)
\(I_1=\displaystyle\frac{P}{Vcosθ}\)
<三相4線式>
\(P=3VI_3cosθ\)
\(I_3=\displaystyle\frac{P}{3Vcosθ}\)
\(\displaystyle\frac{3I_3^2}{2I_1^2}×100=\displaystyle\frac{3×\displaystyle\frac{P^2}{9V^2cos^2θ}}{2×\displaystyle\frac{P^2}{V^2cos^2θ}}×100\)
\(=\displaystyle\frac{\displaystyle\frac{1}{3}}{2}×100\)
\(=\displaystyle\frac{1}{6}×100\)
\(=16.7[\%]\)
したがって、(1)が正解です。