【使いやすさNo.1】電験三種(電力)の過去問解説集2016★動画と図でやさしく説明

電験三種の過去問解説(電力)：2016年(平成28)問17
バランサ接続後の電流と線路損失の変化量(計算)

図のような、線路抵抗をもった100/200V単相3線式配電線路に、力率が100%で電流がそれぞれ30A及び20Aの二つの負荷が接続されている。この配電線路にバランサを接続した場合について、次の(a)及び(b)の問に答えよ。

ただし、バランサの接続前後で負荷電流は変化しないものとし、線路抵抗以外のインピーダンスは無視するものとする。

(a) バランサ接続後a'-b'間に流れる電流の値[A]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1)5

(2)10

(3)20

(4)25

(5)30

(b) バランサ接続前後の線路損失の変化量の値[W]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1)20

(2)65

(3)80

(4)125

(5)145

出典元：一般財団法人電気技術者試験センター

スポンサーリンク

過去問のポイント

バランサを接続することで、電流がどのように変化するのかを知らないと解けません。

解き方自体は簡単なので、変化がわからなかった方も次は間違えないように解けると思います。

(a)バランサ接続後の電流

バランサを接続した際の、各部の電流を図に描き込んでいきましょう。

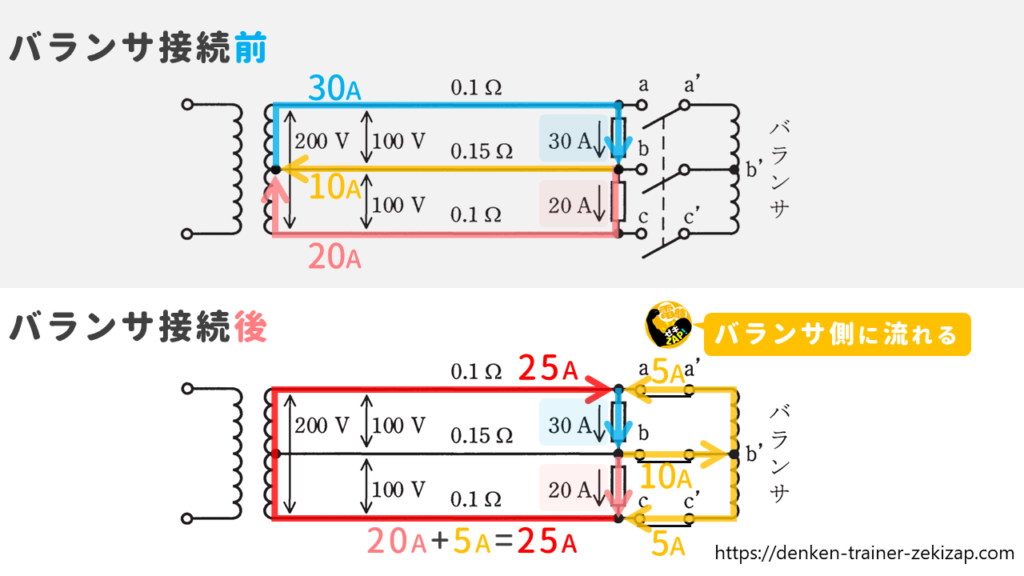
<バランサ接続前>

・中性線を流れる電流

　30-20=10[A]

<バランサ接続後>

・中性線を流れていた電流10Aが、バランサ側に流れる

・バランサ側に流れた10Aはb'で1:1に分かれる

　a'-b'間=5A

　b'-c'間=5A

したがって、(1)が正解です。

(b)バランサ接続前後の線路損失変化

図に記入した各線路の電流と抵抗から、線路損失を求めましょう。

<バランサ接続前>

10A、20A、30Aの電流が流れる線路ごとの損失を足し算しましょう

\(P_{L前}=0.15×10^2+0.1×20^2+0.1×30^2\)

　　 \(=145[W]\)

<バランサ接続後>

25Aの電流が流れる線路が2つあるので、損失を足し算しましょう

\(P_{L後}=0.1×25^2+0.1×25^2\)

　　 \(=125[W]\)

\(変化量 = 145 - 125 =20[W]\)

したがって、(1)が正解です。