【使いやすさNo.1】電験三種(電力)の過去問解説集2016★動画と図でやさしく説明

電験三種の過去問解説(電力)：2016年(平成28)問16
地絡事故及び三相短絡事故による電流(計算)

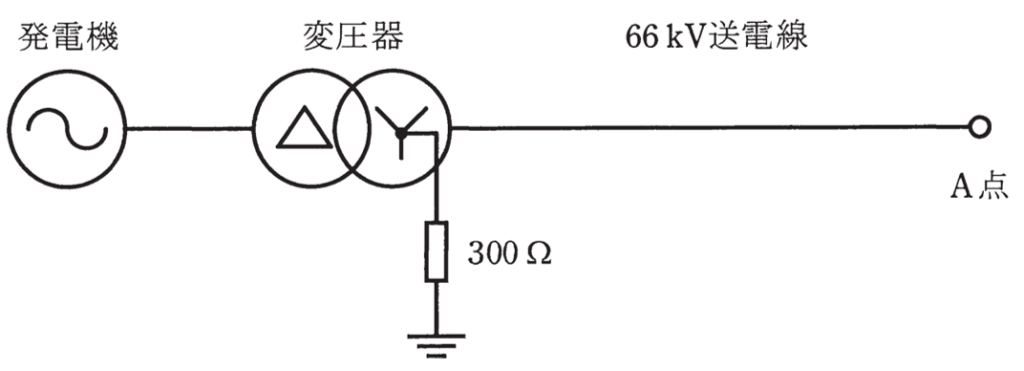
図に示すように、発電機、変圧器と公称電圧66kVで運転される送電線からなる系統があるとき、次の(a)及び(b)の問に答えよ。ただし、中性点接地抵抗は図の変圧器のみに設置され、その値は300Ωとする。

(a) A点で100Ωの抵抗を介して一線地絡事故が発生した。このときの地絡電流の値[A]として、最も近いものを次の(1)～(5)のうちから一つ選べ。
　 ただし、発電機、発電機と変圧器間、変圧器及び送電線のインピーダンスは無視するものとする。

(1)95

(2)127

(3)165

(4)381

(5)508

(b) A点で三相短絡事故が発生した。このときの三相短絡電流の値[A]として、最も近いものを次の(1)～(5)のうちから一つ選べ。
　 ただし、発電機の容量は10000kV・A、出力電圧6.6kV、三相短絡時のリアクタンスは自己容量ベースで25%、変圧器容量は10000KV・A、変圧比は6.6kV/66kV、リアクタンスは自己容量ベースで10%、66kV送電線のリアクタンスは、10000kV・Aベースで5%とする。なお、発電機と変圧器間のインピーダンスは無視する。また、発電機、変圧器及び送電線の抵抗は無視するものとする

(1)33

(2)219

(3)379

(4)656

(5)3019

出典元：一般財団法人電気技術者試験センター

スポンサーリンク

過去問のポイント

一線地絡事故が発生した時の回路を正しく描けること(電圧や抵抗の接続など)や、パーセントインピーダンスの公式が問題を解くポイントです。

今回の問題は計算過程も短く、すぐに解けてしまうので、B問題ではサービス問題となります。

(a)地絡電流

step
1問題の図を描きなおす

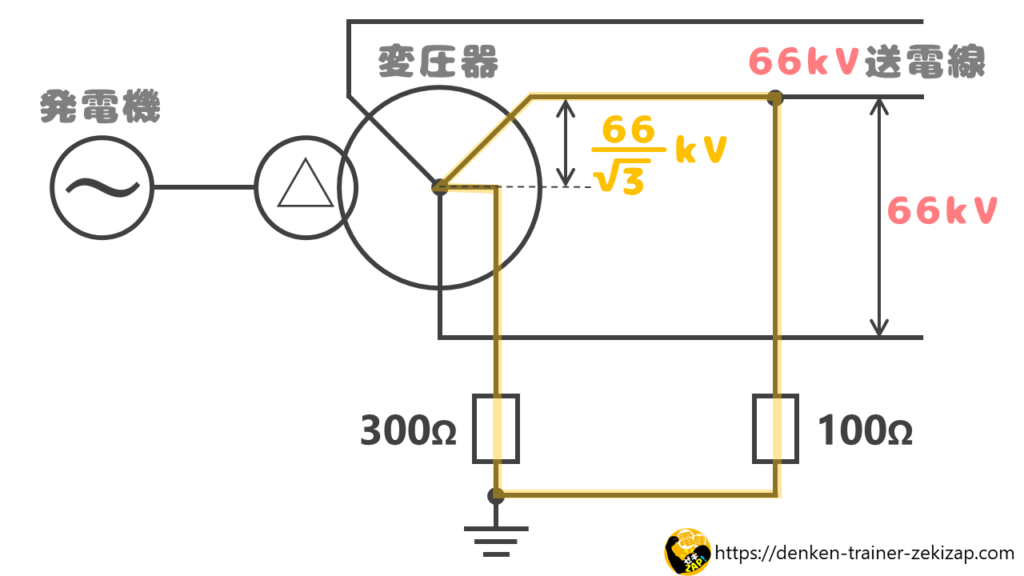
A点で100Ωの抵抗を介して一線地絡事故が発生した状態を図にします。

ちなみに、黄色で囲んだ閉回路の相電圧は、

\(E=\displaystyle\frac{66}{\sqrt{3}}\)

　\(=38.15[kV]\)

となります。

step
2地絡電流を計算

300Ωと100Ωの抵抗が直列接続された回路の電流を求めるだけなので、簡単ですね。

\(I_g=\displaystyle\frac{E}{300+100}\)

　 \(=\displaystyle\frac{38.15×10^3}{400}\)

　 \(=95[A]\)

となり、(1)が正解です。

スポンサーリンク

(b)三相短絡電流

step
1図にパーセントインピーダンスを描き込む

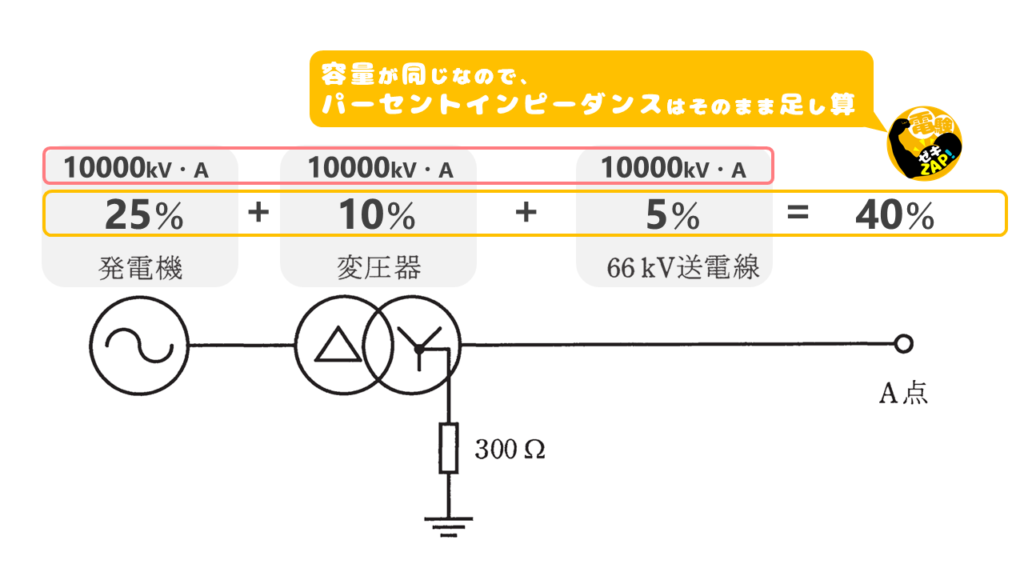
発電機/変圧器/66kV送電線の容量が10000kV・Aで同じなので、A点から見たパーセントインピーダンスはそのまま足し算することができます。

\(\%Z=25+10+5=40[\%]\)

step
2定格電流の計算

\(I_n=\displaystyle\frac{P}{\sqrt{3}V}\)

　 \(=\displaystyle\frac{10000×10^3}{\sqrt{3}×66×10^3}\)

　 \(=87.476[A]\)

step
3三相短絡電流

三相短絡電流は、パーセントインピーダンスの公式から求めることができます。

\(I_s=\displaystyle\frac{I_n}{\%Z}×100\)

　 \(=\displaystyle\frac{87.476}{40}×100\)

　 \(=219[A]\)

したがって、(2)が正解です。