電験三種の過去問解説(電力):2016年(平成28)問1
揚水発電所の電力、所要時間、総合力率(計算)
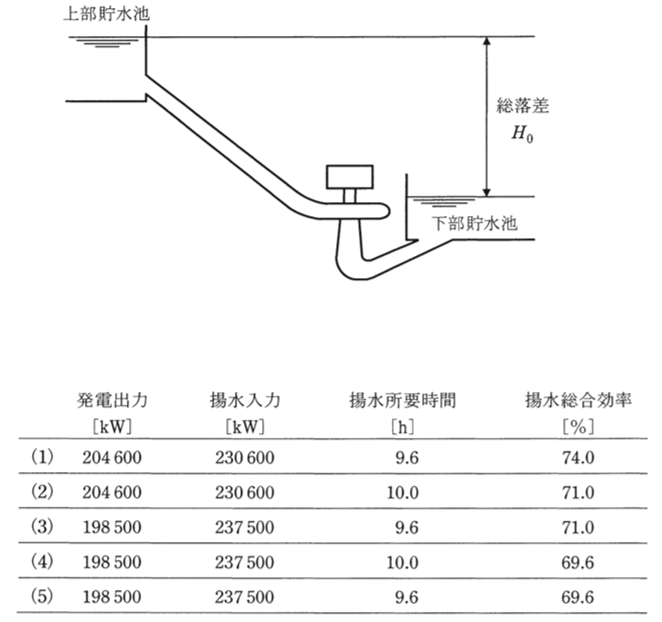
下記の諸元の揚水発電所を、運転中の総落差が変わらず、発電出力、揚水入力ともに一定で運転するものと仮定する。この揚水発電所における発電出力の値[kW]、揚水入力の値[kW]、揚水所要時間の値[h]及び揚水総合効率の値[%]として、最も近い値の組合せを次の(1)~(5)のうちから一つ選べ。
揚水発電所の諸元
総落差 \(H_0=400m\)
発電損失水頭 \(h_G=H_0の3\%\)
揚水損失水頭 \(h_P=H_0の3\%\)
発電使用水量 \(Q_G=60m^3/s\)
揚水量 \(Q_P=50m^3/s\)
発電運転時の効率 \(発電機効率η_G×水車効率η_T=87\%\)
ポンプ運転時の効率 \(電動機効率η_M×ポンプ効率η_P=85\%\)
発電運転時間 \(T_G=8h\)
スポンサーリンク
過去問のポイント
揚水発電所に関する計算問題では、2種類の使用状態(発電と揚水)における問が出題されます。
発電時と揚水時で計算では、効率と有効落差の扱い方が異なることに注意して問題を解きましょう!
発電出力
発電出力の公式
\(P_G=9.8Q_G(H-h_G)η_Gη_T[kW]\)
発電出力の公式に問題文で与えられている数値を正しく代入しましょう。
注意ポイント
発電損失水頭
\(h_G=H_0の3\%=400×0.03=12[m]\)
\(P_G=9.8×60×(400-12)×0.87[kW]\)
\(=198,485[kW]\)
揚水入力
揚水入力の公式
\(P_P=\displaystyle\frac{9.8Q_P(H+h_P)}{η_Mη_P}[kW]\)
揚水入力の公式に問題文で与えられている数値を正しく代入しましょう。
注意ポイント
揚水損失水頭
\(h_P=H_0の3\%=400×0.03=12[m]\)
\(P_P=\displaystyle\frac{9.8×50×(400+12)}{0.85}[kW]\)
\(=\displaystyle\frac{201,880}{0.85}\)
\(=237,506[kW]\)
揚水所要時間
揚水所要時間
揚水所要時間×揚水量=発電運転時間×発電使用水量
揚水所要時間\(T_P\)の計算は、発電に使用した水を揚水で上に戻すイメージ…
つまり、発電と揚水で水量をそろえる感じです。
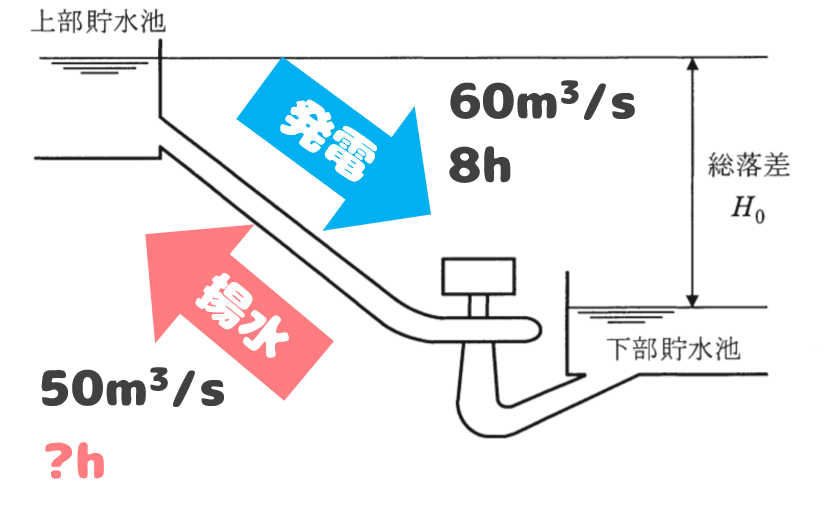
\(50×T_P=60×8\)
\(T_P=\displaystyle\frac{480}{50}\)
\(=9.6[h]\)
揚水総合効率
揚水総合効率
\(揚水総合効率=\displaystyle\frac{H-h_G}{H+h_P}η_Gη_Tη_Mη_P×100[\%]\)
揚水総合効率の公式に問題文で与えられている数値を正しく代入しましょう。
\(揚水総合効率=\displaystyle\frac{400-12}{400+12}×0.87×0.85×100[\%]\)
\(=69.6[\%]\)
したがって、(5)が正解です。