電験三種の過去問解説(電力):2015年(平成27)問17
電力系統の合成線路インピーダンスと送電電力(計算)
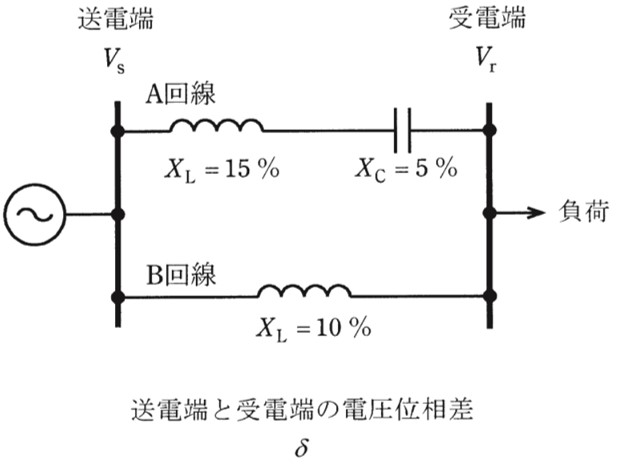
図に示すように、線路インピーダンスが異なるA、B回線で構成される154kV系統があったとする。A回線側にリアクタンス5%の直列コンデンサが設置されているとき、次の(a)及び(b)の問に答えよ。なお、系統の基準容量は、10MV・Aとする。
(a)図に示す系統の合成線路インピーダンスの値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)3.3 (2)5.0 (3)6.0 (4)20.0 (5)30.0 (b)送電端と受電端の電圧位相差δが30度であるとき、この系統での送電電力Pの値[MW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、送電端電圧Vs、受電端電圧Vrは、それぞれ154kVとする。
(1)17 (2)25 (3)83 (4)100 (5)152
スポンサーリンク
過去問のポイント
リアクタンスとコンデンサの直列接続の計算及びコンデンサの並列接続の計算と、送電電力の公式を覚えていれば解ける問題です。
(a)系統の合成線路インピーダンス
系統の合成線路インピーダンスを求めるにあたって、A回線の直列合成線路インピーダンスを計算した後、A-B回線の並列合成線路インピーダンスを求める…といった感じで順番に計算しましょう。
step
1A回線の直列合成線路インピーダンス
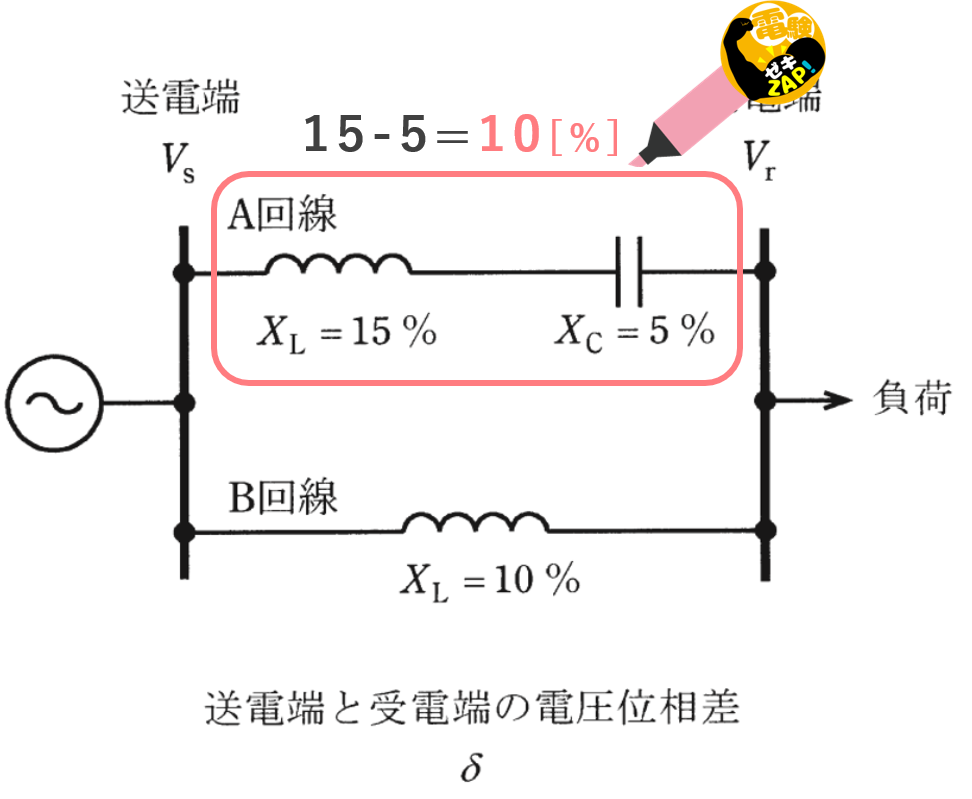
A回線にはリアクタンスとコンデンサが直列に接続されているので、A回線の直列合成線路インピーダンス\(X_A\)[%]は、
\(X_A=X_L-X_C\)
\(=15-5\)
\(=10[\%]\)
となります。
step
2A-B回線の並列合成線路インピーダンス
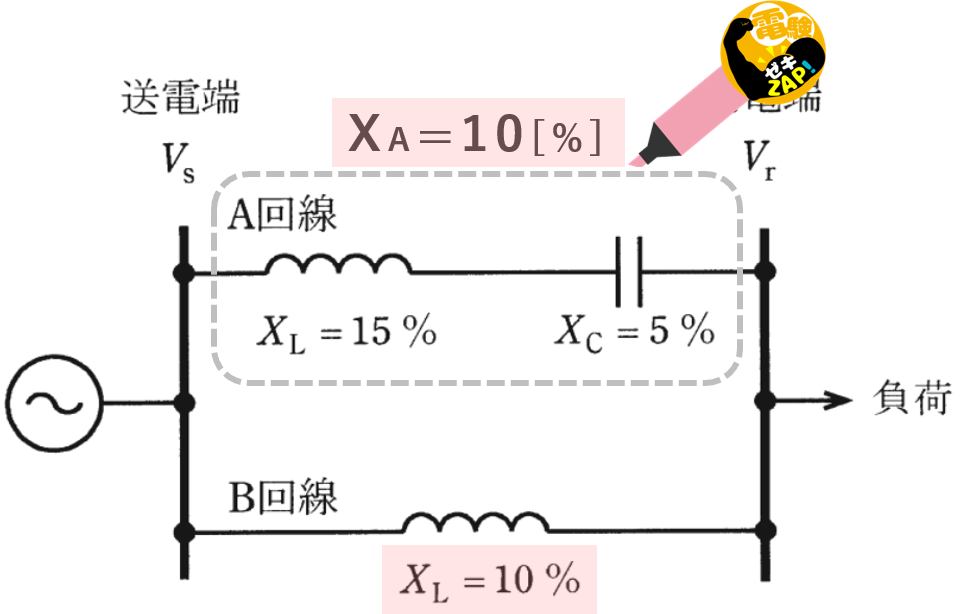
\(\displaystyle\frac{1}{X}=\displaystyle\frac{1}{X_A}+\displaystyle\frac{1}{X_L}\)
\(\displaystyle\frac{1}{X}=\displaystyle\frac{X_A+X_L}{X_AX_L}\)
\(X=\displaystyle\frac{X_AX_L}{X_A+X_L}\)
\(=\displaystyle\frac{10×10}{10+10}\)
\(=5[\%]\)
したがって、(2)が正解です。
スポンサーリンク
(b)送電電力
送電電力
\(P={\displaystyle\frac{V_sV_r}{X}}sinδ[W]\)
\(V_s\):送電端電圧154[kV]
\(V_r\):受電端電圧154[kV]
\(δ\):電圧位相差(相差角)30°
step
1合成抵抗X[Ω]の計算
送電電力の公式に数値を代入すれば解けますが、合成抵抗X[Ω]がわからないため、まずは合成抵抗X[Ω]を求めましょう。
合成抵抗は\(\%X=\displaystyle\frac{\sqrt{3}XI}{V}×100[\%]\) を変換して求めます。
分母と分子に\(V\)をかけましょう!
\(\%X=\displaystyle\frac{\sqrt{3}VIX}{V^2}×100\)
注意ポイント
分母と分子に\(V\)をかけたことで、
分子の一部が基準容量\(P'=\sqrt{3}VI=10[MV・A]\)に変換できることに気づきましょう
\(\%X=\displaystyle\frac{P'X}{V^2}×100\)
\(X=\displaystyle\frac{V^2×\%X}{P'×100}\)
\(=\displaystyle\frac{(154×10^3)^2×5}{10×10^6×10^2}\)
\(=\displaystyle\frac{118.58×10^9}{10^9}\)
\(=118.58[Ω]\)
step
2送電電力の計算
送電電力
\(P={\displaystyle\frac{V_sV_r}{X}}sinδ[W]\)
\(V_s\):送電端電圧154[kV]
\(V_r\):受電端電圧154[kV]
\(δ\):電圧位相差(相差角)30°
\(X\):合成抵抗118.58[Ω]
\(P=\displaystyle\frac{154×10^3×154×10^3}{118.58}×\frac{1}{2}\)
\(=\displaystyle\frac{23716×10^6}{237.16}\)
\(=100×10^6[W]\)
\(=100[MW]\)
したがって、(4)が正解です。