電験三種の過去問解説(理論):2019年(令和元年)問1
点電荷周辺の電位差(計算)
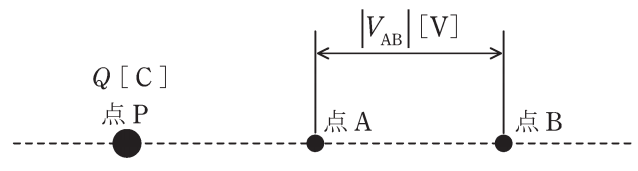
図のように、真空中に点P、点A、点Bが直線状に配置されている
。点PはQ[C]の点電荷を置いた点とし、A- B間に生じる電位差の絶対値を|VAB|[V]とする。次の( a)~(d)の四つの実験を個別に行ったとき、|VAB|[V] の値が最小となるものと最大となるものの実験の組合せとして、正 しいものを次の(1)~(5)のうちから一つ選べ。 [実験内容]
(a)P-A間の距離を2m、A-B間の距離を1mとした。
(b)P-A間の距離を1m、A-B間の距離を2mとした。
(c)P-A間の距離を0.5m、A-B間の距離を1mとした。
(d)P-A間の距離を1m、A-B間の距離を0.5mとした。
(1) (a)と(b) (2) (a)と(c) (3) (a)と(d) (4) (b)と(c) (5) (c)と(d)
スポンサーリンク
過去問解説
\(|V_{AB}|\)とは、点Pの電荷Q[C]によるA点の電位\(V_A\)とB点の電位\(V_B\)の差です。
つまり、\(|V_{AB}|=|V_A-V_B|\)と表せます。
ちなみに、点電荷周辺の電位は下記公式より求められます。
点電荷の電位
\(V=\displaystyle\frac{Q}{4πε_0r}[V]\)
r:点電荷との距離[m]
(a)、(b)、(c)、(d)の実験内容を上記式に代入して、\(|V_{AB}|\)を比較しましょう。
(a)P-A間の距離を2m、A-B間の距離を1mとした
\(|V_{AB}|=|\displaystyle\frac{Q}{4πε_0×2}-\displaystyle\frac{Q}{4πε_0×(2+1)}|\)
\(=|\displaystyle\frac{Q}{8πε_0}-\displaystyle\frac{Q}{12πε_0}|\)
\(=|\displaystyle\frac{3Q}{24πε_0}-\displaystyle\frac{2Q}{24πε_0}|\)
\(=\displaystyle\frac{Q}{24πε_0}\)
(
\(|V_{AB}|=|\displaystyle\frac{Q}{4πε_0×1}-\displaystyle\frac{Q}{4πε_0×(1+2)}|\)
\(=|\displaystyle\frac{Q}{4πε_0}-\displaystyle\frac{Q}{12πε_0}|\)
\(=|\displaystyle\frac{3Q}{12πε_0}-\displaystyle\frac{Q}{12πε_0}|\)
\(=\displaystyle\frac{Q}{6πε_0}\)
(c)
\(|V_{AB}|=|\displaystyle\frac{Q}{4πε_0×0.5}-\displaystyle\frac{Q}{4πε_0×(0.5+1)}|\)
\(=|\displaystyle\frac{Q}{2πε_0}-\displaystyle\frac{Q}{6πε_0}|\)
\(=|\displaystyle\frac{3Q}{6πε_0}-\displaystyle\frac{Q}{6πε_0}|\)
\(=\displaystyle\frac{Q}{3πε_0}\)
(d)
\(|V_{AB}|=|\displaystyle\frac{Q}{4πε_0×1}-\displaystyle\frac{Q}{4πε_0×(1+0.5)}|\)
\(=|\displaystyle\frac{Q}{4πε_0}-\displaystyle\frac{Q}{6πε_0}|\)
\(=|\displaystyle\frac{3Q}{12πε_0}-\displaystyle\frac{2Q}{12πε_0}|\)
\(=\displaystyle\frac{Q}{12πε_0}\)
(a)、(b)、(c)、(d)の実験内容から求めた\(|V_{AB}|\)は、
| (a)\(\displaystyle\frac{Q}{24πε_0}\) | (b)\(\displaystyle\frac{Q}{6πε_0}\) | (c)\(\displaystyle\frac{Q}{3πε_0}\) | (d)\(\displaystyle\frac{Q}{12πε_0}\) |
となったため、(c)が最大、(a)が最小なので、(2)が正解です。