【ヒント掲載で使い易い】電験三種(理論)の過去問題集2019★動画と図でやさしく解説

電験三種の過去問解説(理論)：2019年(令和元年)問5
直流回路の電位差(計算)

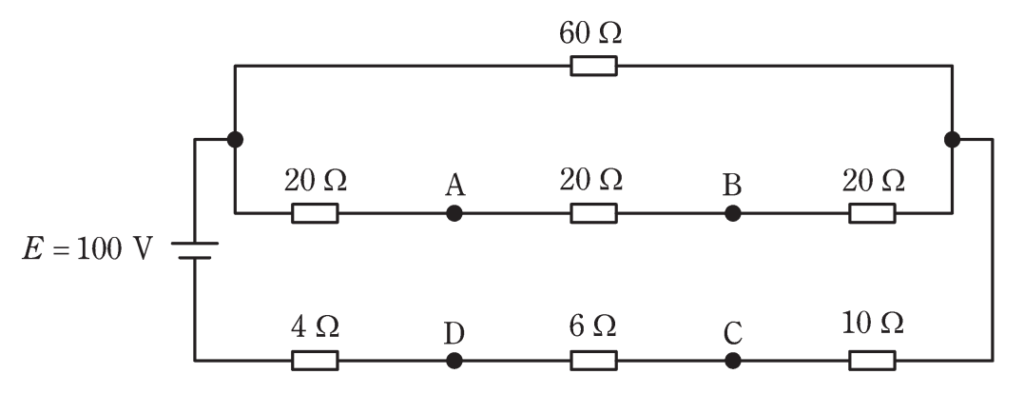
図のように、七つの抵抗及び電圧 E=100V の直流電源からなる回路がある。この回路において、A-D間、B-C間の各電位差を測定した。このとき、A-D間の電位差の大きさ[V]及びB-C間の電位差の大きさ[V]の組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

出典元：一般財団法人電気技術者試験センター

スポンサーリンク

過去問解説

電位差を求めるためには各抵抗の電圧を求める必要がありますが、まずは大きなくくりで抵抗にかかる電圧を求めましょう。

20Ωの抵抗が3個直列接続されている部分と、4Ωと6Ωと10Ωの抵抗が直列接続されている部分があるので、それぞれの合成抵抗は、

\(R_1=20+20+20=60\)

\(R_2=4+6+10=20\)

となります。

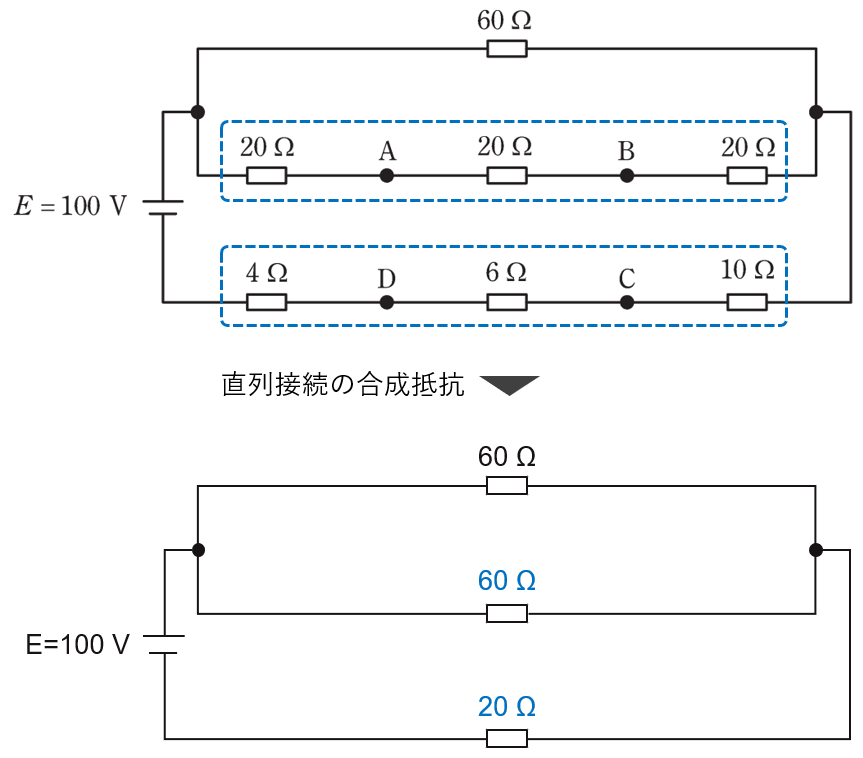
つづいて、60Ωの抵抗が並列接続されているので、合成抵抗は

\(\displaystyle\frac{1}{R_3}=\displaystyle\frac{1}{60}+\displaystyle\frac{1}{60}\)

 \(R_3=30\)

となります。

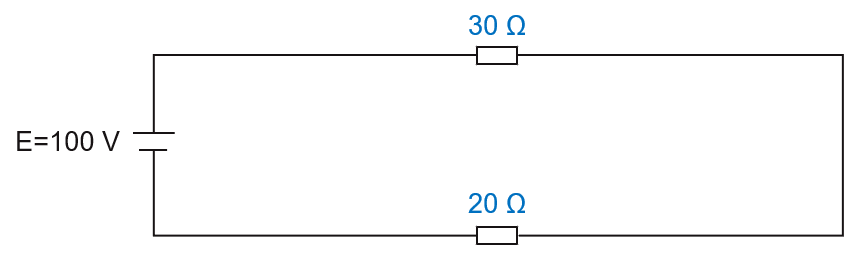
ここで、各抵抗の電圧を求めます。

\(V=\displaystyle\frac{30}{20+30}×100=60[V]\)

\(V=\displaystyle\frac{20}{20+30}×100=40[V]\)

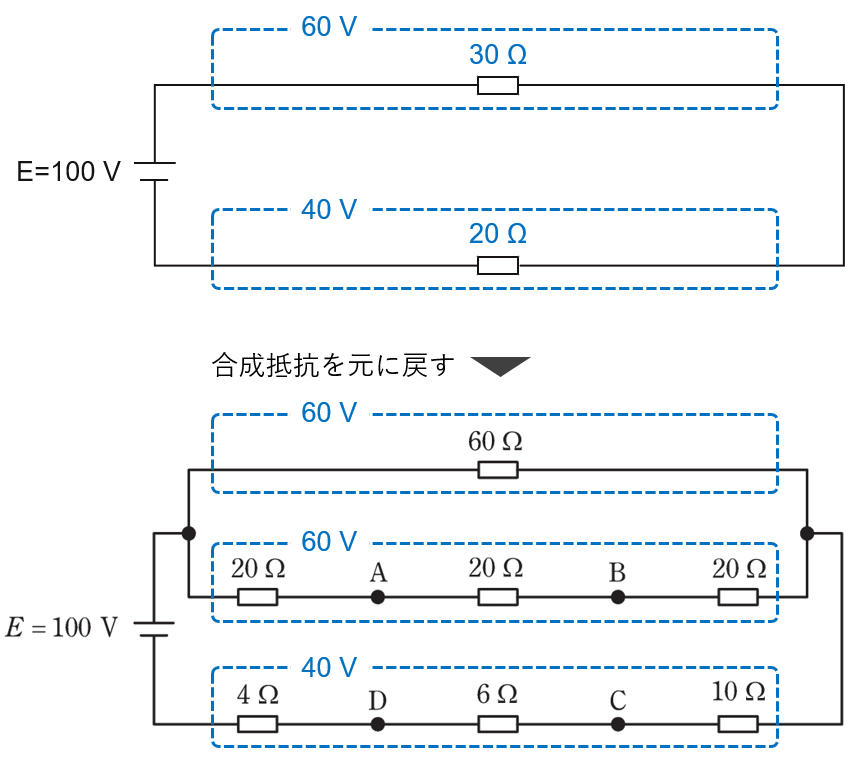
20Ωの抵抗が3つ直列接続されている部分は、60Vの電圧が3等分されるため、

\(V=\displaystyle\frac{60}{3}=20[V]\)

となります。

4Ωと6Ωと10Ωの抵抗が直列接続されている部分は、それぞれ計算して求めましょう。

\(V_{4Ω}=\displaystyle\frac{4×40}{4+6+10}=8[V]\)

\(V_{6Ω}=\displaystyle\frac{6×40}{4+6+10}=12[V]\)

\(V_{10Ω}=\displaystyle\frac{10×40}{4+6+10}=20[V]\)

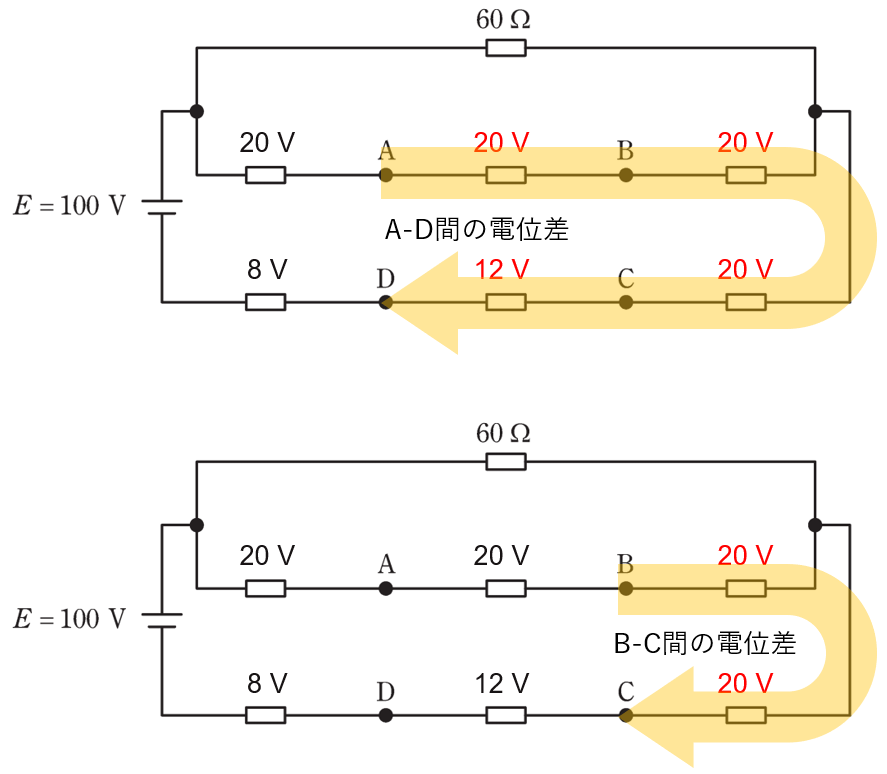
各抵抗の電圧が求められたので、A-D間、B-C間の電位差を求めましょう。

\(ΔV_{AD}=20+20+20+12=72[V]\)

\(ΔV_{BC}=20+20=40[V]\)

したがって、(5)が正解です。