【ヒント掲載で使い易い】電験三種(理論)の過去問題集2019★動画と図でやさしく解説

電験三種の過去問解説(理論)：2019年(令和元年)問12
放出された点電荷が極板間中心に達する時間(計算)

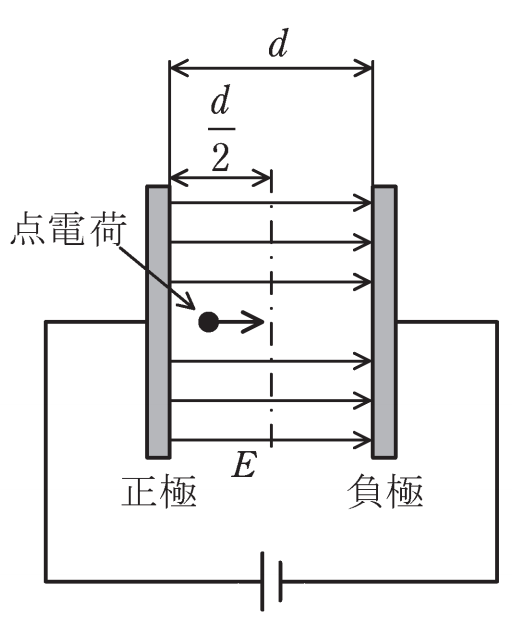
図のように、極板間の距離d[m]の平行板導体が真空中に置かれ、極板間に強さE[V/m]の一様な電界が生じている。質量m[kg]、電荷量q(>0)[C]の点電荷が正極から放出されてから、極板間の中心\(\displaystyle\frac{d}{2}[m]\)に達するまでの時間t[s]を表す式として、正しいものを次の(1)～(5)のうちから一つ選べ。
ただし、点電荷の速度は光束より十分小さく、初速度は0m/sとする。また、重力の影響は無視できるものとし、平行板導体は十分大きいものとする。

\((1)\sqrt{\displaystyle\frac{md}{qE}}\)

\((2)\sqrt{\displaystyle\frac{2md}{qE}}\)

\((3)\sqrt{\displaystyle\frac{qEd}{m}}\)

\((4)\sqrt{\displaystyle\frac{qE}{md}}\)

\((5)\sqrt{\displaystyle\frac{2qE}{md}}\)

出典元：一般財団法人電気技術者試験センター

スポンサーリンク

過去問解説

2種類の方法で速度を表す式を求めて、速度が互いに等しくなることを利用して極板間の中心\(\displaystyle\frac{d}{2}[m]\)に達するまでの時間t[s]を表す式を求めます。

step
1電界が電荷に与えたエネルギーW₁と運動エネルギーW₂

電界が電荷に与えたエネルギーW₁と極板間中心の運動エネルギーW₂は等しくなるので、

　  \(W_2=W_1\)

\(\displaystyle\frac{1}{2}mv^2=\displaystyle\frac{qEd}{2}\)

　　  \(v=\sqrt{\displaystyle\frac{qEd}{m}}\)・・・①式

step
2電界中の電荷に働く力と運動方程式

上記式より、

\(ma=qE\)

　\(a=\displaystyle\frac{qE}{m}\)

初速度0の電荷が加速度\(a=\displaystyle\frac{qE}{m}\)で、極板間の中心に達した時の速度は

\(v=at=\displaystyle\frac{qEt}{m}\)・・・②式

①、②式より、

\(\displaystyle\frac{qEt}{m}=\sqrt{\displaystyle\frac{qEd}{m}}\)

　　\(t=\sqrt{\displaystyle\frac{qEd}{m}}×\displaystyle\frac{m}{qE}\)

　　   \(=\sqrt{\displaystyle\frac{qEd}{m}×\displaystyle\frac{m^2}{q^2E^2}}\)

　　   \(=\sqrt{\displaystyle\frac{md}{qE}}\)

したがって、(1)が正解です。