【ヒント掲載で使い易い】電験三種(機械)の過去問題集2019★動画と図でやさしく解説

電験三種の過去問解説(機械)：2019年(令和元年)問15
同期発電機の並行運転(計算)

並行運転しているA及びBの2台の三相同期発電機がある。それぞれの発電機の負荷分担が同じ7300kWであり、端子電圧が6600Vのとき、三相同期発電機Aの負荷電流I_Aが1000A、三相同期発電機Bの負荷電流I_Bが800Aであった。損失は無視できるものとして、次の(a)及び(b)の問に答えよ。

(a)三相同期発電機Aの力率の値[%]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1)48

(2)64

(3)67

(4)77

(5)80

(b)2台の発電機の合計の負荷が調整の前後で変わらずに一定に保たれているものとして、この状態から三相同期発電機A及びBの励磁及び駆動機の出力を調整し、三相同期発電機Aの負荷電流は調整前と同じ1000Aとし、力率は100%とした。このときの三相同期発電機Bの力率の値[%]として、最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし、端子電圧は変わらないものとする。

(1)22

(2)50

(3)71

(4)87

(5)100

出典元：一般財団法人電気技術者試験センター

スポンサーリンク

過去問解説

(a)：三相同期発電機Aの力率の値

三相同期発電機Aの力率は下記式で求められます。

有効電力P_Aは問題文より7300[kW]です。

つぎに、三相同期発電機Aの皮相電力S_Aは下記式で求められます。

問題文より各数値を代入すると、

\(S_A=\sqrt3×6600×1000=11431.5[kV・A]\)

となります。

有効電力と皮相電力の値を力率の式に代入しましょう。

\(cosθ_A=\displaystyle\frac{P_A}{S_A}×100\)

　　　  \(=\displaystyle\frac{7300}{11431.5}×100\)

　　　  \(=64[\%]\)

従って、(2)が正解です。

(b)：三相同期発電機Bの力率の値

まずは、問題文の内容をイメージしやすいように図で整理してみましょう。

step
1調整前

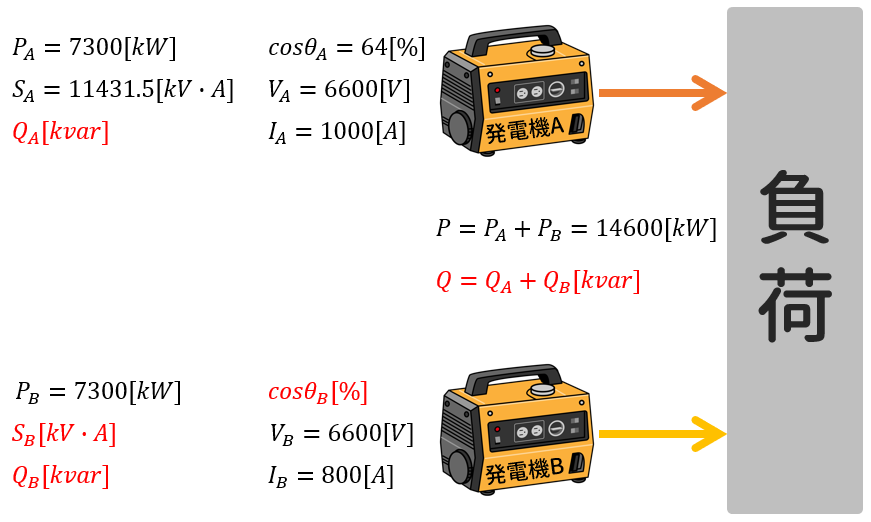
AとBの発電機の負荷分担が7300[kW]で等しいことがポイントです。

よって、合計負荷容量は、

\(P=P_A+P_B\)

　 \(=7300+7300\)

　 \(=14600[kW]\)

となります。

続いて、無効電力Qの合計値を下記式を利用して求めます。

先ずは、発電機Aの無効電力ですが、

\(Q_A=P_Atanθ_A\)

　　\(=P_A×\displaystyle\frac{sinθ_A}{cosθ_A}\)

　　\(=P_A×\displaystyle\frac{\sqrt{1-cos^2θ_A}}{cosθ_A}\)

　　\(=7300×\displaystyle\frac{\sqrt{1-0.64^2}}{0.64}\)

　　\(=8764[kvar]\)

次に発電機Bですが、皮相電力S_Bと力率cosθ_Bを求めてから、無効電力Q_Bを求めましょう。

\(S_B=\sqrt3×6600×800=9145[kV・A]\)

\(cosθ=\displaystyle\frac{P_B}{S_B}×100[\%]\)

　　  \(=\displaystyle\frac{7300}{9145}×100\)

　　  \(=9.8[\%]\)

\(Q_B=P_Btanθ_B\)

　　\(=P_B×\displaystyle\frac{sinθ_B}{cosθ_B}\)

　　\(=P_B×\displaystyle\frac{\sqrt{1-cos^2θ_B}}{cosθ_B}\)

　　\(=7300×\displaystyle\frac{\sqrt{1-0.798^2}}{0.798}\)

　　\(=5513[kvar]\)

したがって、無効電力の合計値は

\(Q=Q_A+Q_B\)

　 \(=8761+5513\)

　 \(=14277[kvar]\)

となります。

step
2調整後

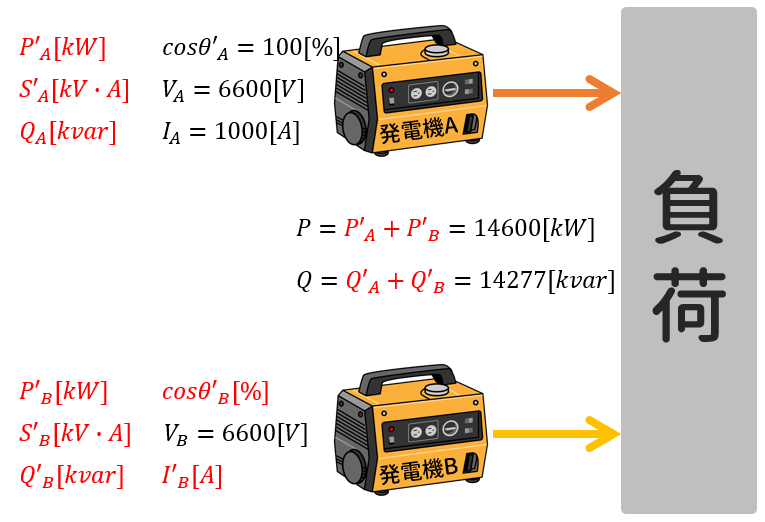
変化する部分と変化しない部分があることに注意して図を描きましょう！

先ずは、発電機Aの方から整理していきましょう。

調整後は力率を100[%]としたので、無効電力Q'_Aがゼロとなります。

また、有効電力P'_Aは、

\(P'_A=\sqrt3V_AI_Acosθ'_A\)

　　\(=\sqrt3×6600×800×1\)

　　\(=11431.5[kW]\)

となります。

つづいて、発電機Bの方を有効電力P'_Bと無効電力Q'_Bを整理してから力率を求めましょう。

\(P'_B=P-P'_A\)

　　\(=14600-11431.5\)

　　\(=3168.5[kW]\)

\(Q'_B=Q-Q'_A\)

　　\(=14277-0\)

　　\(=14277[kvar]\)

よって、力率cosθ'_Bは

\(cosθ'_B=\displaystyle\frac{P'_B}{S'_B}×100\)

　　　 \(=\displaystyle\frac{P'_B}{\sqrt{P'^2_B+Q'^2_B}}×100\)

　　　 \(=\displaystyle\frac{3168.5}{\sqrt{3168.5^2+14277^2}}×100\)

　　　 \(=\displaystyle\frac{3168.5}{14624.37}×100\)

　　　 \(=22[\%]\)

したがって、(1)が正解です。