【ヒント掲載で使い易い】電験三種(機械)の過去問題集2019★動画と図でやさしく解説

電験三種の過去問解説(機械)：2019年(令和元年)問13
周波数伝達関数の式(計算)

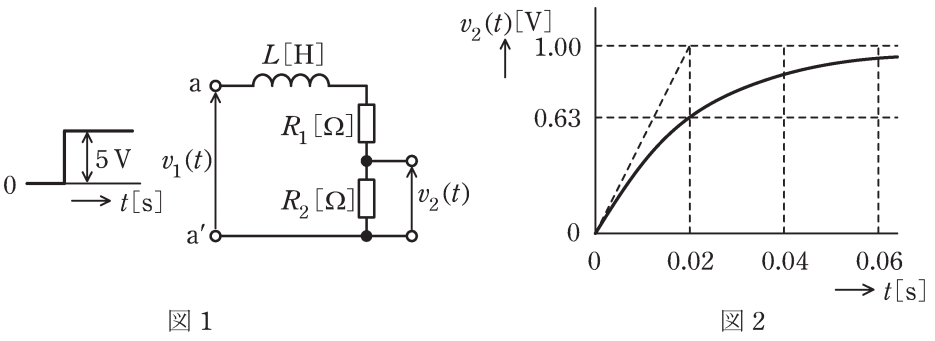
図1に示すR-L回路において、端子a-a'間に5Vの階段状のステップ電圧v₁(t)[V]を加えたとき、抵抗R₂[Ω]に発生する電圧をv₂(t)[V]とすると、v₂(t)は図2のようになった。この回路のR₁[Ω]、R₂[Ω]及びL[H]の値と、入力をv₁(t)、出力をv₂(t)としたときの周波数伝達関数G(jω)の式として、正しいものを次の(1)～(5)のうちから一つ選べ。

	R1	R2	L	G(jω)
(1)	80	20	0.2	\(\displaystyle\frac{0.5}{1+j0.2ω}\)
(2)	40	10	1.0	\(\displaystyle\frac{0.5}{1+j0.02ω}\)
(3)	8	2	0.1	\(\displaystyle\frac{0.2}{1+j0.2ω}\)
(4)	4	1	0.1	\(\displaystyle\frac{0.2}{1+j0.02ω}\)
(5)	0.8	0.2	1.0	\(\displaystyle\frac{0.2}{1+j0.2ω}\)

出典元：一般財団法人電気技術者試験センター

スポンサーリンク

過去問解説

問題を見ると、R₁、R₂、Lの値を求めたくなると思いますが、電験三種の知識では求められません…

そこで、周波数伝達関数G(jω)の式を求めていきましょう。ちなみに、基本式は下記で表されます。

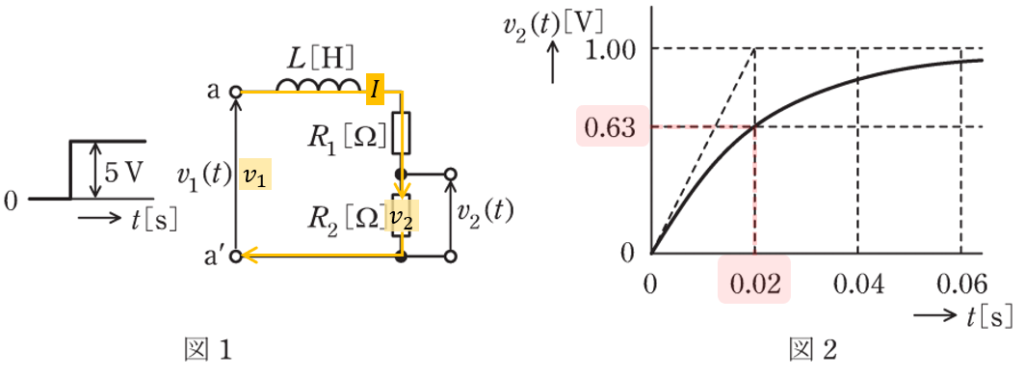
回路を流れる電流をIとすると、電圧v₁、v₂は下記式で表せます。

\(v_1=(R_1+R_2+jωL)I\)

\(v_2=R_2I\)

これらを周波数伝達関数の式に代入すると、

\(G(jω)=\displaystyle\frac{R_2I}{(R_1+R_2+jωL)I}\)

　　　  \(=\displaystyle\frac{R_2}{R_1+R_2+jωL}・・・①式\)

となります。

図２より、v₂は十分時間が経過すると1Vになることがわかるので、R1の電圧v_R1は

\(v_{R1}=5-1=4[V]\)

となります。

分圧比の関係から、

\(R_1:R_2=v_{R1}:v_2\)

\(R_1:R_2=4:1\)

　　  \(R_1=4R_2・・・②式\)

となります。

次に、時定数τは下記式で求められます。

図2よりτ=0.02であることがわかるので、

 \(0.02=\displaystyle\frac{L}{R_1+R_2}\)

 \(0.02=\displaystyle\frac{L}{4R_2+R_2}\)

\(\displaystyle\frac{L}{5R_2}=0.02\)

　  \(L=0.1R_2・・・③式\)

となります。

ここで、①式に②式と③式を代入しましょう。

\(G(jω)=\displaystyle\frac{R_2}{4R_2+R_2+jω0.1R_2}\)

　　　  \(=\displaystyle\frac{R_2}{5R_2+jω0.1R_2}\)

　　　  \(=\displaystyle\frac{1}{5+j0.1ω}\)

　　　  \(=\displaystyle\frac{\displaystyle\frac{1}{5}}{\displaystyle\frac{5}{5}+j\displaystyle\frac{0.1}{5}ω}\)

　　　  \(=\displaystyle\frac{0.2}{1+j0.02ω}\)

したがって、(4)が正解です。