電験三種の過去問解説(電力)：2018年(平成30)問16
太陽光発電設備接続前の電圧と、接続後の電流(計算)
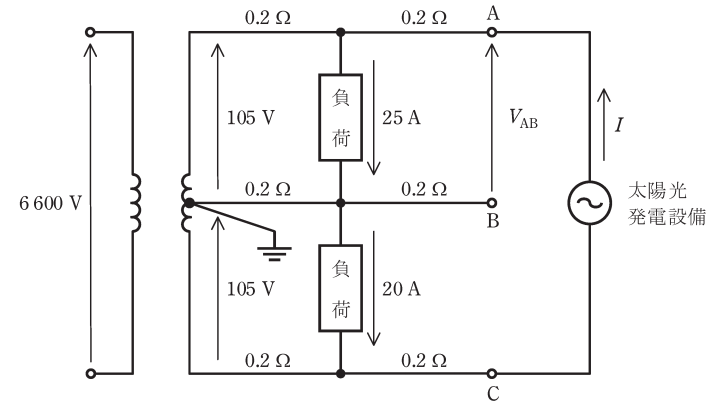
図のように、電圧線及び中性線の各部の抵抗が0.2Ωの単相3線式低圧配電線路において、末端のAC間に太陽光発電設備が接続されている。各部の電圧及び電流が図に示された値であるとき、次の(a)及び(b)の問に答えよ。ただし、負荷は定電流特性で力率は1、太陽光発電設備の出力(交流)は電流\(I[A]\)、力率1で一定とする。また、線路のインピーダンスは抵抗とし、図示していないインピーダンスは無視するものとする。
(a) 太陽光発電設備を接続する前のAB間の端子電圧\(V_{AB}\)の値[V]として、最も近いものを次の(1)～(5)のうちから一つ選べ。
(1)96 (2)99 (3)100 (4)101 (5)104 (b)太陽光発電設備を接続したところ、AB間の端子電圧\(V_{AB}[V]\)が\(107V\)となった。このときの太陽光発電設備の出力電流(交流)\(I\)の値[A]として、最も近いものを次の(1)～(5)のうちから一つ選べ。
(1)5 (2)15 (3)20 (4)25 (5)30
+ ヒントを見る
キルヒホッフの第二法則
ある閉回路の電源電圧（起電力）の総和と、負荷で消費される電圧（電圧降下）の総和は等しい
スポンサーリンク
過去問のポイント
回路図のある問題では、どこに何Aの電流が流れているのか、回路図に記入しながら問題を解きましょう。
難しそうに見える問題も丁寧に解けば、大丈夫です♪
(a)太陽光発電設備接続前のAB間の端子電圧
AB間の端子電圧を求めるにあたって、少し回路図に追記しておきましょう。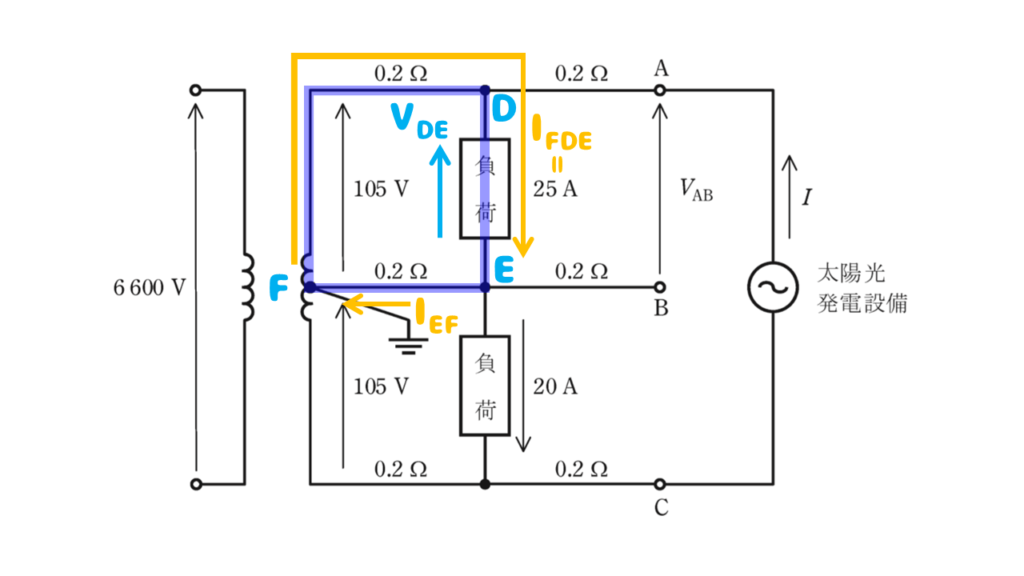
回路図にDEFを追記しました。
AB間の端子電圧は25Aの電流が流れる負荷の電圧\(V_{DE}\)と等しくなります。
ココに注意
理論の勉強もあわせて進めるようにしましょう。
キルヒホッフの第二法則を使って青色の閉回路から端子電圧\(V_{DE}\)を求めます
\(105=0.2I_{FDE}+V_{DE}+0.2I_{EF}\)
\(105=0.2×25+V_{DE}+0.2I_{EF}\)
\(100=V_{DE}+0.2I_{EF}\)
\(V_{DE}=100-0.2I_{EF}\)・・・①式
次に\(I_{EF}\)を求めて①式に代入しましょう
\(I_{FDE}\)は\(I_{EF}\)と\(20A\)に分岐していることを式にしましょう
\(I_{FDE}=I_{EF}+20\)
\(25=I_{EF}+20\)
\(I_{EF}=5\)
\(I_{EF}=5[A]\)を①式に代入しましょう
\(V_{DE}=100-0.2×5\)
\(V_{DE}=99[V]\)
したがって、(2)が正解です。
スポンサーリンク
(b)太陽光発電設備接続後の出力電流
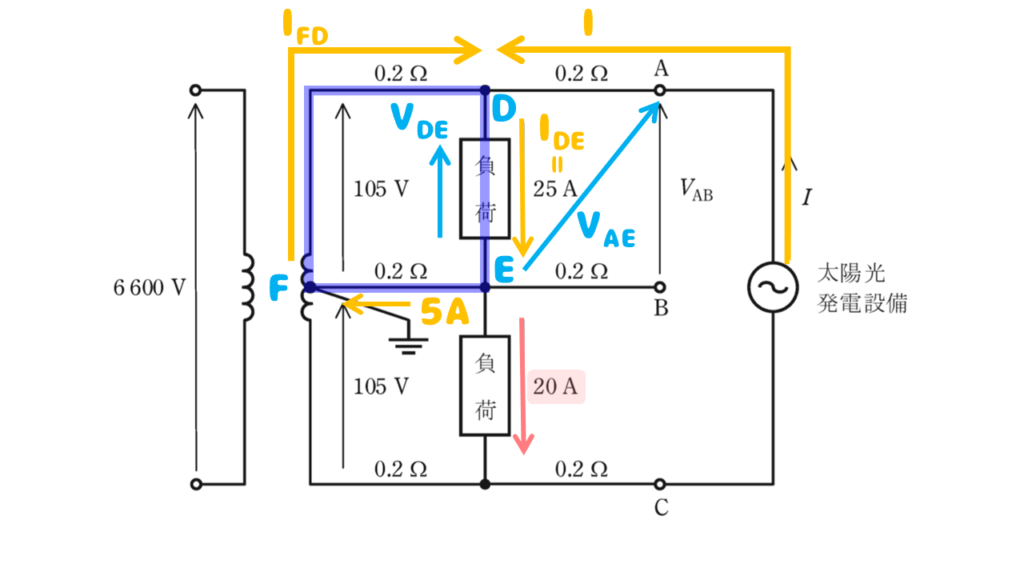
ココに注意
今回求めたい出力電流\(I\)を用いて、\(V_{DE}\)を求める式を書くと…
\(V_{DE}=V_{AE}-0.2I\)・・・②式
と表すことができます。
ちなみに、問題文より\(V_{AB}=107[V]\)と記載されていますが、
\(V_{AB}=107=V_{AE}\)の関係を利用して、②式に代入しましょう
(わからない方は、理論の勉強をやりましょう)
\(V_{DE}=107-0.2I\)
キルヒホッフの第二法則を使って青色の閉回路から出力電流\(I\)を求めます
\(105=0.2I_{FD}+V_{DE}+0.2×5\)
\(105=0.2(25-I)+(107-0.2I)+1\)
\(0.4I=8\)
\(I=20[A]\)
したがって、(3)が正解です。