【使いやすさNo.1】電験三種(電力)の過去問解説集2017★動画と図でやさしく説明

電験三種の過去問解説(電力)：2017年(平成29)問16
三相1回線ケーブルの対地静電容量と線間静電容量の比、及び充電電流(計算)

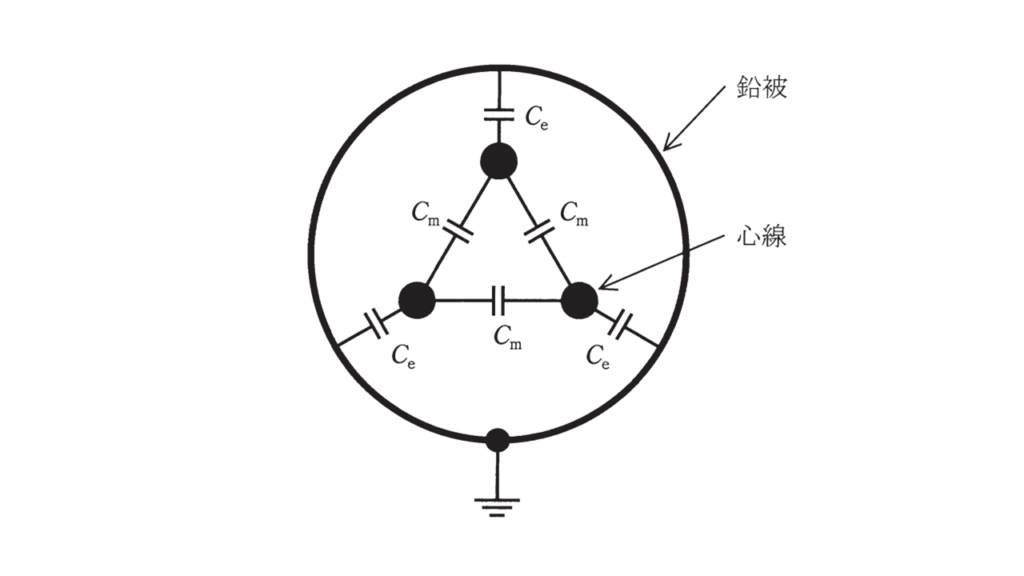
図に示すように、対地静電容量Ce[F]、線間静電容量Cm[F]からなる定格電圧E[V]の三相1回線のケーブルがある。
今、受電端を開放した状態で、送電端で三つの心線を一括してこれと大地間に定格電圧E[V]の\(\displaystyle\frac{1}{\sqrt3}\)倍の交流電圧を加えて充電すると全充電電流は90Aであった。
次に、二つの心線の受電端・送電端を接地し、受電端を開放した残りの心線と大地間に定格電圧E[V]の\(\displaystyle\frac{1}{\sqrt3}\)倍の交流電圧を送電端に加えて充電するとこの心線に流れる充電電流は45Aであった。
次の(a)及び(b)の問に答えよ。
ただし、ケーブルの鉛被は接地されているとする。また、各心線の抵抗とインダクタンスは無視するものとする。なお、定格電圧及び交流電圧の周波数は、一定の商用周波数とする。

(a)対地静電容量Ce[F]と線間静電容量Cm[F]の比\(\displaystyle\frac{Ce}{Cm}\)として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1)0.5

(2)1.0

(3)1.5

(4)2.0

(5)4.0

(b)このケーブルの受電端を全て開放して定格の三相電圧を送電端に加えたときに1線に流れる充電電流の値[A]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1)52.5

(2)75

(3)105

(4)120

(5)135

出典元：一般財団法人電気技術者試験センター

スポンサーリンク

過去問のポイント

問題の図を等価回路に変換するため、『理論』の知識が要求される難易度の高い問題です。

最初は解けない方も多いと思いますが、何度も繰り返し解いて、解き方を身につけましょう！

(a)対地静電容量Ce[F]と線間静電容量Cm[F]の比

この段階では、充電電流の比から静電容量の比が求められる理由がわからないと思いますが、それぞれの充電電流を求めていきましょう。

step
1三つの心線を一括した場合の充電電流

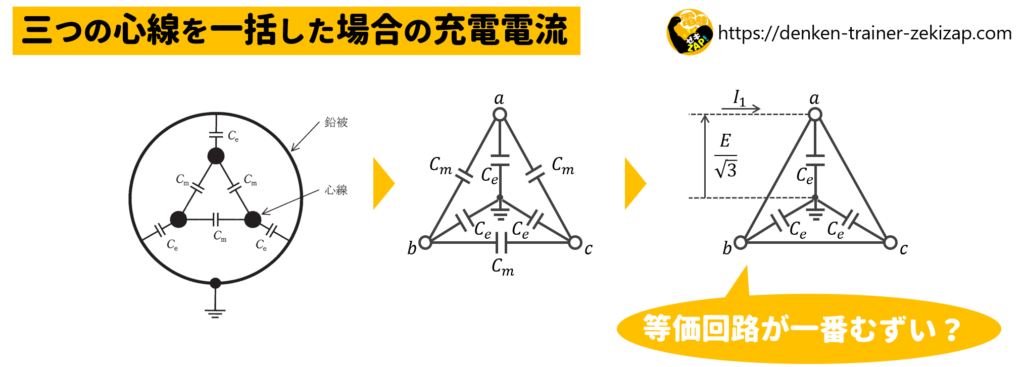
三つの心線を一括して、これと大地間の定格電圧E[V]の\(\displaystyle\frac{1}{\sqrt3}\)倍の交流電圧を加えた場合の等価回路は上図となります。

図を参考に充電電流を表す式を書いてみましょう。

\(I_1=jω3C_e×\displaystyle\frac{E}{\sqrt3}\)

step
2二つの心線を接地した場合

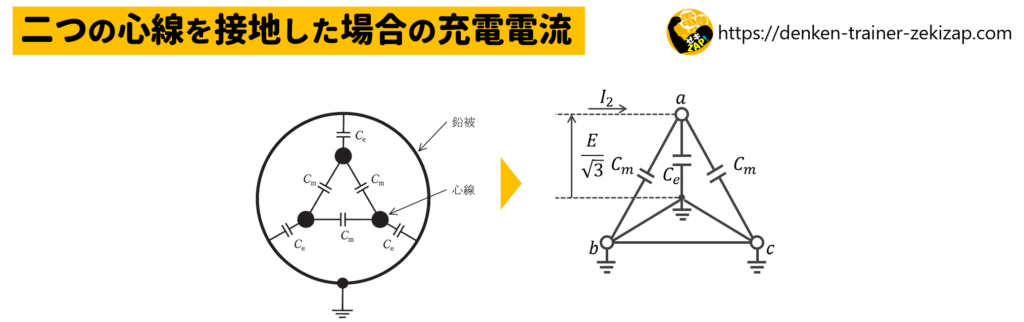
二つの心線の受電端・送電端を接地し、受電端を開放した残りの心線と大地間に定格電圧E[V]の\(\displaystyle\frac{1}{\sqrt3}\)倍の交流電圧を送電端に加えた場合の等価回路は上図となります。

図を参考に充電電流を表す式を書いてみましょう。

\(I_2=jω(2C_m+C_e)×\displaystyle\frac{E}{\sqrt3}\)

step
3対地静電容量Ce[F]と線間静電容量Cm[F]の比

求めた充電電流を表す式を比にしてみましょう。ちなみに、各値は下記の通りです。

　　　　　　　　　　　　　　　   \(I_1:I_2=90:45\)

\(jω3C_e×\displaystyle\frac{E}{\sqrt3}:jω(2C_m+C_e)×\displaystyle\frac{E}{\sqrt3}=2:1\)

　　　　　　　　　　  \(3C_e:2C_m+C_e=2:1\)

　　　　　　　　　　　　\(2(2C_m+C_e)=3C_e\)

　　　　　　　　　　　　    \(4C_m+2C_e=3C_e\)

　　　　　　　　　　　　　　　　　  \(C_e=4C_m\)

　　　　　　　　　　　　　　　　   \(\displaystyle\frac{C_e}{C_m}=4\)

したがって、(5)が正解です。

(b)1線に流れる充電電流の値

step
1受電端を全て開放して定格の三相電圧を送電端に加えた場合

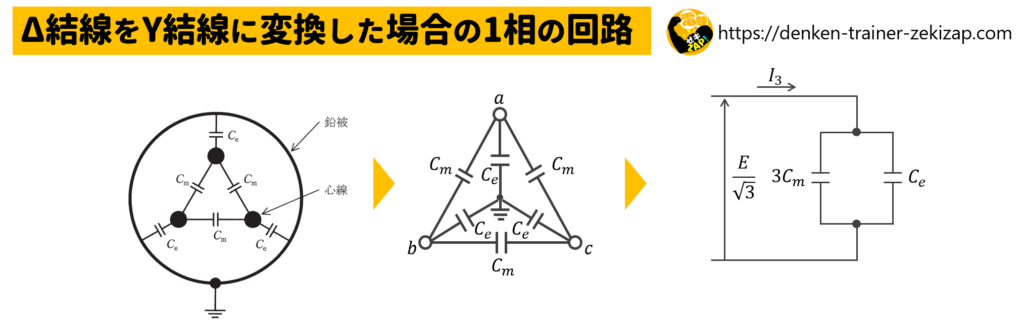
受電端を全て開放して定格の三相電圧を送電端に加えた場合の等価回路は上図となります。

図を参考に充電電流を表す式を書いてみましょう。

\(I_3=jω(3C_m+C_e)×\displaystyle\frac{E}{\sqrt3}\)

(a)で求めた\(\displaystyle\frac{C_e}{C_m}=4\)の関係より、\(C_m=\displaystyle\frac{C_e}{4}\)を代入しましょう。

\(I_3=jω(3×\displaystyle\frac{C_e}{4}+C_e)×\displaystyle\frac{E}{\sqrt3}\)

　  \(=jω×\displaystyle\frac{7C_e}{4}×\displaystyle\frac{E}{\sqrt3}\)

step
21線に流れる充電電流の値

充電電流\(I_3\)と、(a)で求めた充電電流\(I_1\)を比の関係でまとめましょう。

 \(I_1:I_3=jω3C_e×\displaystyle\frac{E}{\sqrt3}:jω×\displaystyle\frac{7C_e}{4}×\displaystyle\frac{E}{\sqrt3}\)

\(90:I_3=3:\displaystyle\frac{7}{4}\)

 \(3×I_3=90×\displaystyle\frac{7}{4}\)

　　 \(I_3=52.5[A]\)

したがって、(1)が正解です。