電験三種の過去問解説(電力)：2016年(平成28)問15
汽力発電所のタービン効率と発電機効率(計算)
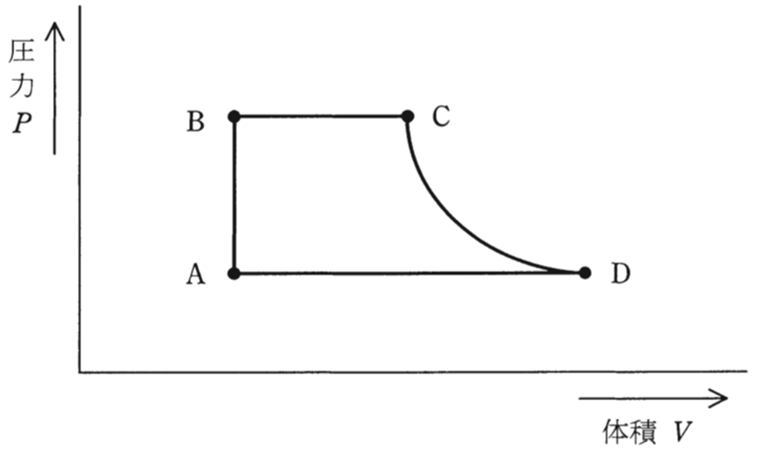
図は、あるランキンサイクルによる汽力発電所のP-V線図である。この発電所が、A点の比エンタルピー\(140kJ/kg\)、B点の比エンタルピー\(150kJ/kg\)、C点の比エンタルピー\(3380kJ/kg\)、D点の比エンタルピー\(2560kJ/kg\)、蒸気タービンの使用蒸気量\(100t/h\)、蒸気タービン出力\(18MW\)で運転しているとき、次の(a)及び(b)の問に答えよ。
(a) タービン効率の値[%]として、最も近いものを次の(1)～(5)のうちから一つ選べ。
(1)58.4 (2)66.8 (3)79.0 (4)95.3 (5)96.7 (b) この発電所の送電端電力16MW、所内比率5%のとき、発電機効率の値[%]として、最も近いものを次の(1)～(5)のうちから一つ選べ。
(1)84.7 (2)88.6 (3)88.9 (4)89.2 (5)93.6
+ ヒントを見る
イラストを描きながら解くと、頭の中が整理されて解きやすいかもしれません。
スポンサーリンク
過去問のポイント
汽力発電所に関する問題は、穴埋め/論説/計算の3パターンがあります。
公式を暗記することも大切ですが、汽力発電所の簡易的なイラストを描けるようになっておくと、必要な設備に関する問題に対応できるだけでなく、計算過程が見えてくるのでオススメです。
(a)タービン効率
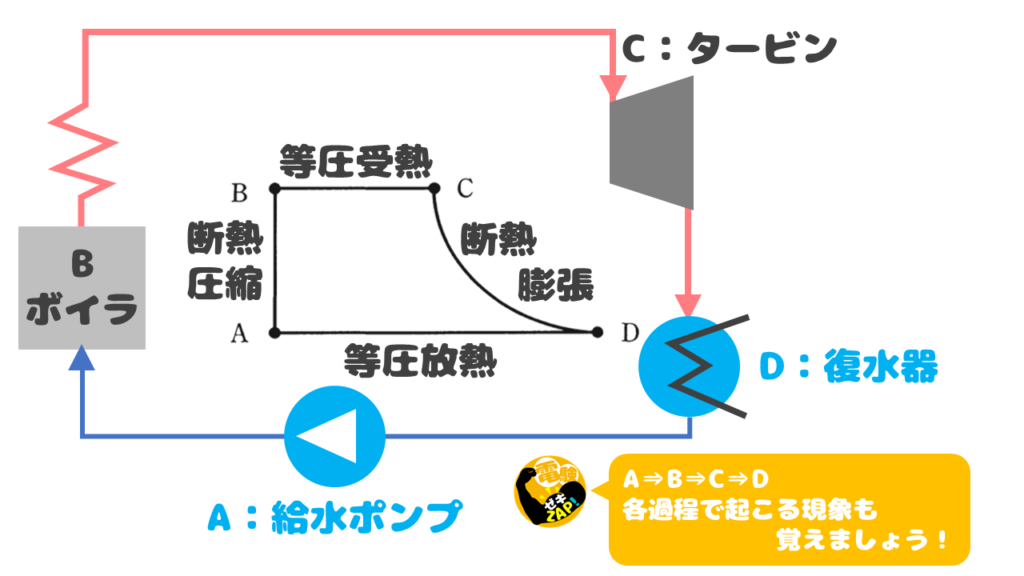
タービン効率は入力と出力の関係で求められます。
タービン効率
\(η_T=\displaystyle\frac{タービンの機械的出力}{蒸気がタービンに与えるエネルギー}×100[\%]\)
問題文より、タービンの機械的出力は18MWなので、蒸気がタービンに与えるエネルギーを求めましょう。
蒸気がタービンに与えるエネルギー
蒸気がタービンに与えるエネルギー = 比エンタルピー × 使用蒸気量
注意ポイント(比エンタルピーの取り扱い)
タービンの仕事はC ➡ Dの過程(断熱膨張)
したがって、蒸気タービンに与えられるエネルギーは、
\(P_{in}=(3380-2560)×1.0×10^5\)
\(=8.2×10^7[kJ/h]\)
\(=\displaystyle\frac{8.2×10^7}{3600}[kW]\)
\(=22.78×10^3[kW]\)
タービン効率の公式に求めた数値を代入しましょう
\(η_T=\displaystyle\frac{18×10^3[kW]}{22.78×10^3[kW]}×100\)
\(=79[\%]\)
したがって、(3)が正解です。
スポンサーリンク
(b)発電機効率
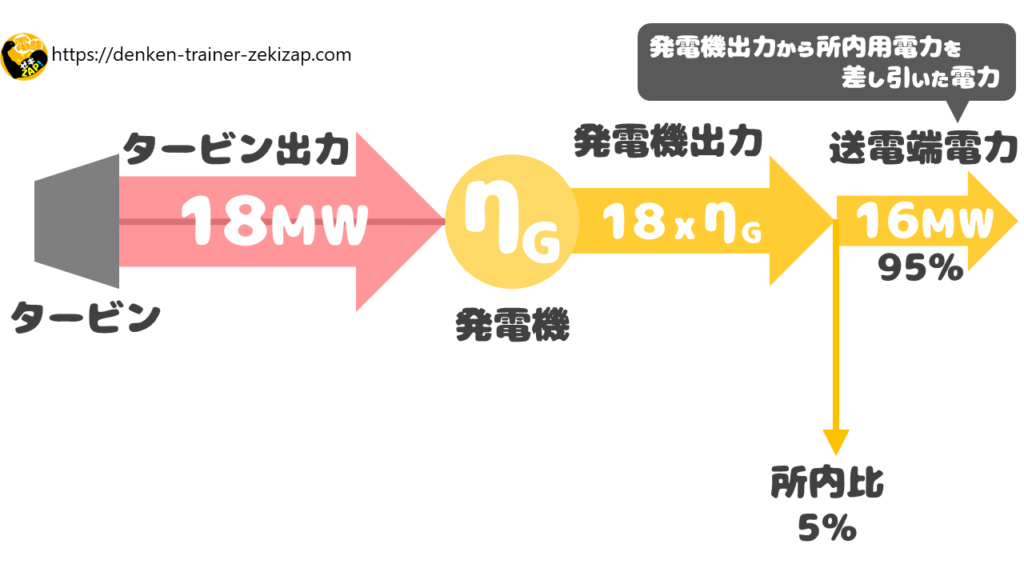
参考
・送電端電力 = 発電機出力 × (1 - 所内比)
・発電機出力 = タービン出力 × 発電機効率
上記の関係を整理すると、
\(送電端電力 = (タービン出力×発電機効率)×(1-所内比)\)
\(16=18×η_G×(1-0.05)\)
\(η_G=\displaystyle\frac{16}{18×0.95}\)
\(=0.936\)
\(➡ 93.6[\%]\)
したがって、(5)が正解です。