電験三種の過去問解説(電力):2015年(平成27)問16
三相3線式変電設備の無効電力と電圧降下(計算)
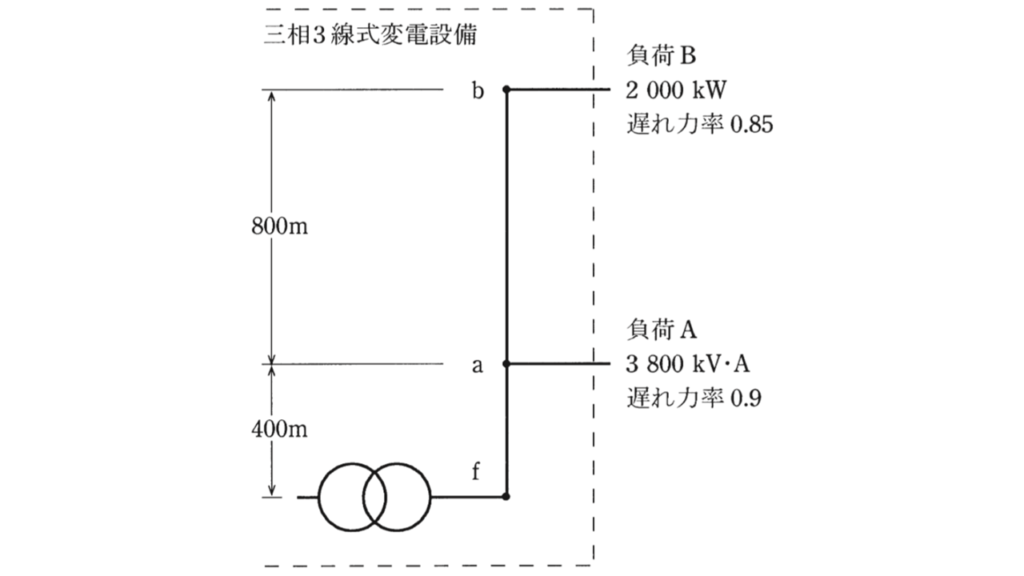
図は、三相3線式変電設備を単線図で表したものである。
現在、この変電設備は、a点から3800kV・A、遅れ力率0.9の負荷Aと、b点から2000kW、遅れ力率0.85の負荷Bに電力を供給している。b点の線間電圧の測定値が22000Vであるとき、次の(a)及び(b)の問に答えよ。
なお、f点とa点の間は400m、a点とb点の間は800mで、電線1条当たりの抵抗とリアクタンスは1km当たり0.24Ωと0.18Ωとする。また、負荷は平衡三相負荷とする。
(a)負荷Aと負荷Bで消費される無効電力の合計値[kvar]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)2710 (2)2900 (3)3080 (4)4880 (5)5120 (b)f-b間の線間電圧の電圧降下\(V_{fb}\)の値[V]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、送電端電圧と受電端電圧との相差角が小さいとして得られる近似式を用いて解答すること。
(1)23 (2)33 (3)59 (4)81 (5)101
スポンサーリンク
過去問のポイント
電力の三角形を描いて、有効電力、皮相電力、無効電力を丁寧にまとめながら計算すると解きやすいかもしれません。
とはいえ、かなり計算過程が長いので、解き方の手順が頭の中に入っていないと解答までたどり着けません…。解けなかった方は何回か繰り返し解くことをオススメします。
負荷Aと負荷Bで消費される無効電力の合計値
問題で与えられている情報をもとに、負荷Aと負荷Bの無効電力をそれぞれ求めて、足し合わせましょう。
step
1負荷Aの無効電力
無効電力の求め方
無効電力[kvar] = 皮相電力[kV・A] × sinθ
\(Q_A=S_Asinθ_A\)
\(=S_A\sqrt{1-cos^2θ_A}\)
\(=3800\sqrt{1-0.9^2}\)
\(=3800\sqrt{0.19}\)
\(=1657[kvar]\)
step
2負荷Bの無効電力
無効電力の求め方
無効電力[kvar] = 有効電力[kW] × tanθ
\(Q_B=P_Btanθ_B\)
\(=P_B\displaystyle\frac{sinθ_B}{cosθ_B}\)
\(=P_B\displaystyle\frac{\sqrt{1-cos^2θ_B}}{cosθ_B}\)
\(=2000\displaystyle\frac{\sqrt{1-0.85^2}}{0.85}\)
\(=2000\displaystyle\frac{\sqrt{0.2775}}{0.85}\)
\(=2000×0.6197\)
\(=1239[kvar]\)
step
3無効電力の合計値
\(Q_A+Q_B=1657+1239=2896[kvar]\)
したがって、最も近い(2)2900が正解です。
スポンサーリンク
(b)f-b間の線間電圧の電圧降下
f-b間の電圧降下は、f-a間とa-b間の電圧降下をそれぞれ求めて、合計しましょう。
三相3線式の電圧降下
\(V_{fb}=V_{fa}+V_{ab}[V]\)
\(V_{fa}=\sqrt{3}(I_A+I_B)(R_{fa}cosθ_A+X_{fa}sinθ_A)[V]\)
\(V_{ab}=\sqrt{3}I_B(R_{ab}cosθ_B+X_{ab}sinθ_B)[V]\)
step
1a-b間の線間電圧降下
電圧降下Vab
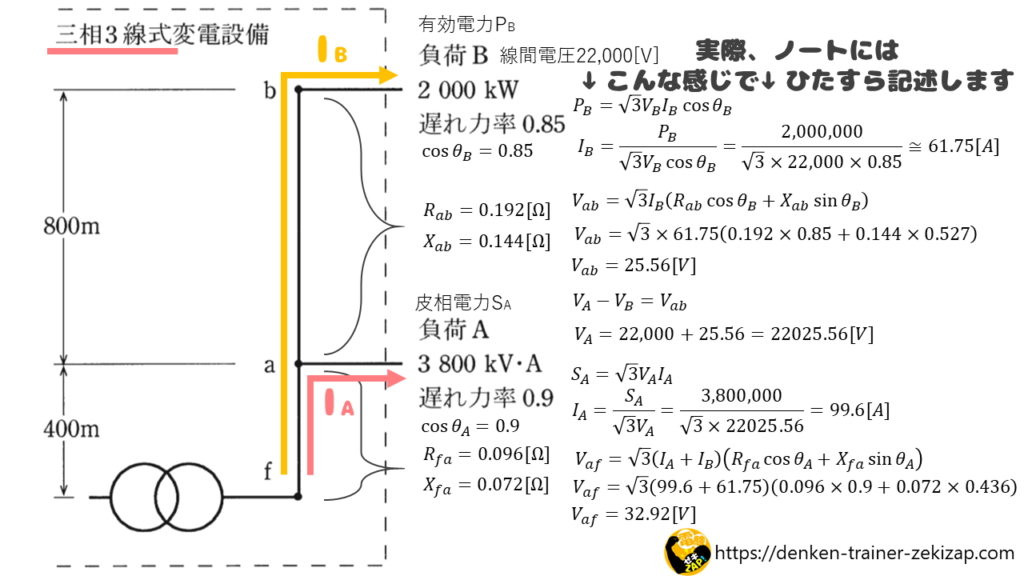
\(V_{ab}=\sqrt{3}I_B(R_{ab}cosθ_B+X_{ab}sinθ_B)\)
\(I_B\)がわからないので、最初に\(I_B\)を求めましょう。
\(P_B=\sqrt{3}V_BI_Bcosθ_B\)より、
\(I_B=\displaystyle\frac{P_B}{\sqrt{3}V_Bcosθ_B}\)
\(=\displaystyle\frac{2,000,000}{\sqrt{3}×22,000×0.85}\)
\(=61.75[A]\)
電圧降下の公式に代入します。
\(V_{ab}=\sqrt{3}I_B(R_{ab}cosθ_B+X_{ab}sinθ_B)\)
\(=\sqrt{3}×61.75(0.192×0.85+0.144×0.527)\)
\(=\sqrt{3}×61.75×0.239\)
\(=25.56[V]\)
step
2f-a間の線間電圧降下
電圧降下Vfa
\(V_{fa}=\sqrt{3}(I_A+I_B)(R_{fa}cosθ_A+X_{fa}sinθ_A)[V]\)
\(I_A\)がわからないので、最初に\(I_A\)を求めましょう。
\(S_A=\sqrt{3}V_AI_A\)より、
\(I_A=\displaystyle\frac{S_A}{\sqrt{3}V_A}\)
\(=\displaystyle\frac{S_A}{\sqrt{3}(V_{ab}+V_B}\)
\(=\displaystyle\frac{3,800,000}{\sqrt{3}(22,000+25.56}\)
\(=99.6[A]\)
電圧降下の公式に代入します。
\(V_{fa}=\sqrt{3}(I_A+I_B)(R_{fa}cosθ_A+X_{fa}sinθ_A)[V]\)
\(=\sqrt{3}(99.6+61.75)(0.096×0.9+0.072×0.436)\)
\(=\sqrt{3}×161.35×0.117792\)
\(=32.92[V]\)
step
3f-b間の線間電圧降下
\(V_{fb}=V_{fa}+V_{ab}\)
\(=32.92+25.56\)
\(=58.48[V]\)
したがって、最も近い(3)59が正解です。