【ヒント掲載で使い易い】電験三種(機械)の過去問題集2019★動画と図でやさしく解説

電験三種の過去問解説(機械)：2019年(令和元年)問1
直流電動機の回転速度(計算)

直流電源に接続された永久磁石界磁の直流電動機に一定トルクの負荷がつながっている。電機子抵抗が1.00Ωである。回転速度が1000min^-1のとき、電源電圧は120V、電流は20Aであった。
この電源電圧を100Vに変化させたときの回転速度の値[min^-1]として、最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし、電機子反作用及びブラシ、整流子における電圧降下は無視できるものとする。

(1)200

(2)400

(3)600

(4)800

(5)1000

出典元：一般財団法人電気技術者試験センター

スポンサーリンク

過去問解説

先ずは、イメージしやすいように直流電動機の等価回路を描いてみましょう。

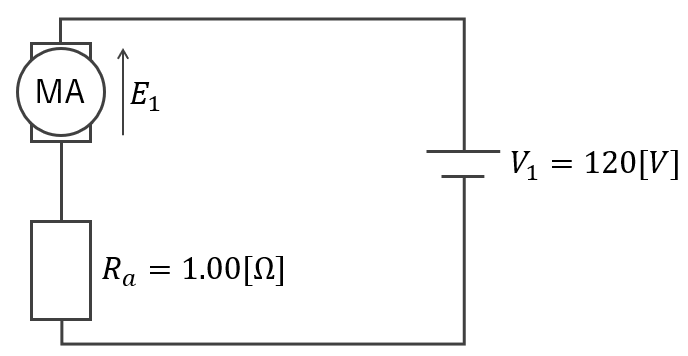
等価回路を見てわかる通り、逆起電力E₁は

\(E_1=V-R_aI_a\)

　   \(=120-1×20\)

　   \(=100[V]\)

となる。

次に、電源電圧を100[V]に変化させたときの回転速度を求めていきましょう。

下記式のように『逆起電力Eが回転速度Nと比例する関係』を利用します。

ちなみに、電源電圧100Vのときの逆起電力E₂は

となるため、

\(E_2=V_2-R_aI_a\)

　   \(=100-1×20\)

　   \(=80[V]\)

逆起電力と回転速度の式に各数値を代入しましょう。

\(E_1:N_1=E_2:N_2\)

　\(E_1N_2=E_2N_1\)

　　  \(N_2=\displaystyle\frac{E_2N_1}{E_1}\)

　　　　  \(=\displaystyle\frac{80×1000}{100}\)

　　　　  \(=800[min^{-1}]\)

したがって、(4)が正解です。