令和2年度(2020年):第三種電気主任技術者試験(理論)問6
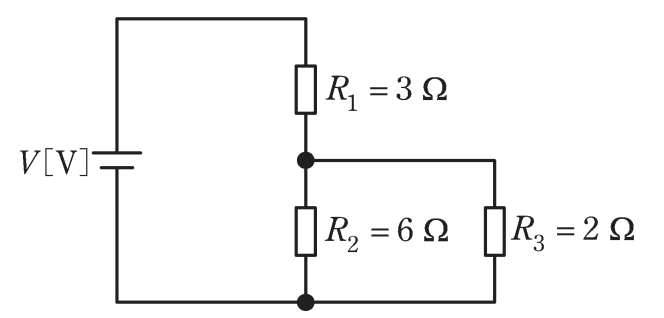
図のように、三つの抵抗\(R_1=3Ω\)、\(R_2=6Ω\)、\(R_3=2Ω\)と電圧V[V]の直流電源からなる回路がある。抵抗\(R_1\)、\(R_2\)、\(R_3\)の消費電力をそれぞれ\(P_1[W]\)、\(P_2[W]\)、\(P_3[W]\)とするとき、その大きさの大きい順として、正しいものを次の(1)~(5)のうちから一つ選べ。
(1)\(P_1>P_2>P_3\)
(2)\(P_1>P_3>P_2\)
(3)\(P_2>P_1>P_3\)
(4)\(P_2>P_3>P_1\)
(5)\(P_3>P_1>P_2\)
動画解説
過去問の解説(2020年理論問6)
抵抗\(R_1\)、\(R_2\)、\(R_3\)の消費電力の大きい順番で正しいものを選ぶ問題です。
まずは、各抵抗を流れる電流(\(I_1\)、\(I_2\)、\(I_3\))を図に記入しましょう!
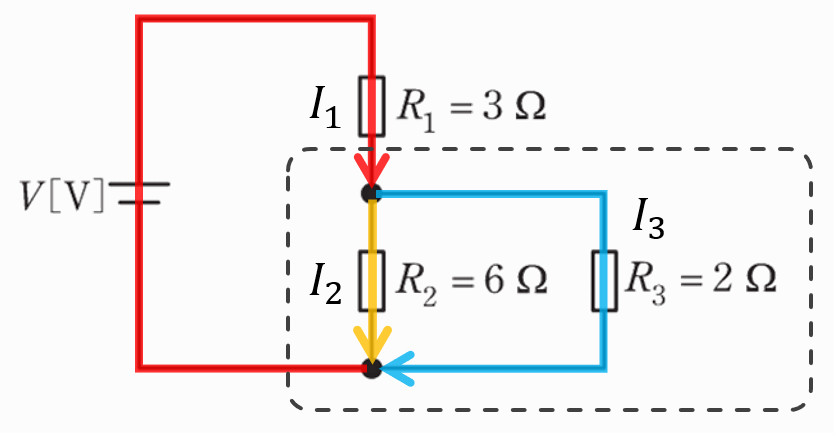
この時、各抵抗の消費電力は、
抵抗\(R_1\)の消費電力\(P_1\)
\(P_1=R_1I_1^2=3I_1^2\)
抵抗\(R_2\)の消費電力\(P_2\)
\(P_2=R_2I_2^2=6I_2^2\)
抵抗\(R_3\)の消費電力\(P_3\)
\(P_3=R_3I_3^2=2I_3^2\)
と表せますが、この状態では消費電力の大きさを比較できないので、電流の表記を統一しましょう。
(今回は\(I_1\)と\(I_2\)を\(I_3\)に変換して解いてみます)
それでは、\(R_2\)と\(R_3\)の並列接続部分を見てみましょう。

並列回路では電圧が等しいので、
\(R_2I_2=R_3I_3\)
と表すことができます。この式を整理すると…
\(I_2=\displaystyle\frac{R_3I_3}{R_2}\)
\(=\displaystyle\frac{2I_3}{6}\)
\(=\displaystyle\frac{I_3}{3}\)
となります。
次に、『分流された電流の合計値』は『元の電流値』となるため、\(I_2\)と\(I_3\)の合計は\(I_1\)と等しくなります。
\(I_1=I_2+I_3\)
\(=\displaystyle\frac{I_3}{3}+I_3\)
\(=\displaystyle\frac{4I_3}{3}\)
最後に、最初に求めた消費電力の式に\(I_1\)と\(I_2\)を代入しましょう!
抵抗R1の消費電力P1
\(P_1=3I_1^2\)
\(=3×(\displaystyle\frac{4I_3}{3})^2\)
\(=3×\displaystyle\frac{16}{9}I_3^2\)
\(=5.3I_3^2\)
抵抗R2の消費電力P2
\(P_2=6I_2^2\)
\(=6×(\displaystyle\frac{I_3}{3})^2\)
\(=6×\displaystyle\frac{1}{9}I_3^2\)
\(=0.67I_3^2\)
抵抗R3の消費電力P3
\(P_3=2I_3^2\)
各抵抗の消費電力が\(I_3\)を含む式で表せたので、大きさを比較すると、
\(P_1>P_3>P_2\)
となり、(2)が正解です。