電験三種の過去問解説(機械):2019年(令和元年)問8
変圧器の循環電流(計算)
2台の単相変圧器があり、それぞれ、巻数比(一次巻数/二次巻数
)が30.1、30.0、二次側に換算した巻線抵抗及び漏れリア クタンスからなるインピーダンスが(0.013+j0.022) Ω、(0.010+j0.020)Ωである。この2台の変圧器を並列接続し二次側を無負荷として、 一次側に6600Vを加えた。この2台の変圧器の二次巻線間を循 環して流れる電流の値[A]として、最も近いものを次の(1)~ (5)のうちか一つ選べ。ただし、 励磁回路のアドミタンスの影響は無視するものとする。
(1)4.1 (2)11.2 (3)15.3 (4)30.6 (5)61.3
スポンサーリンク
過去問解説
変圧器の巻数比aと変圧比の関係は下記式で表される。
巻数比と変圧比
\(a=\displaystyle\frac{V_1}{V_2}\)
\(a:巻数比\)
\(V_1:一次電圧\)
\(V_2:二次電圧\)
上記式を用いて、まずは各変圧器の二次電圧を計算しましょう。
\(V_{A2}=\displaystyle\frac{V_{A1}}{a_A}\)
\(=\displaystyle\frac{6600}{30.1}\)
\(=219.27[V]\)
\(V_{B2}=\displaystyle\frac{V_{B1}}{a_B}\)
\(=\displaystyle\frac{6600}{30}\)
\(=220[V]\)
ポイント
並列接続した2台の変圧器の二次電圧が異なるので、循環電流が生じます
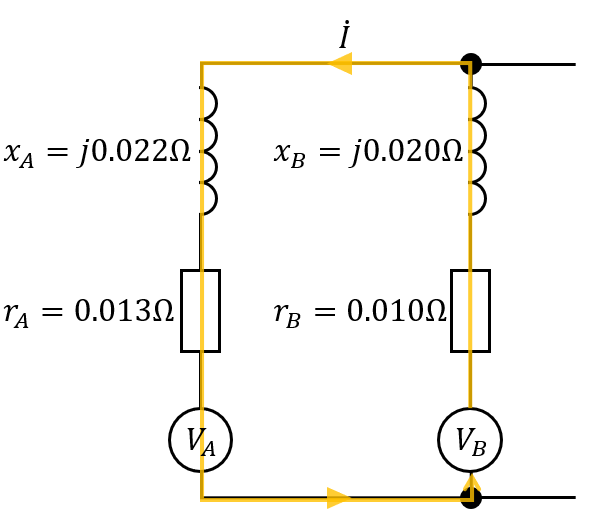
回路図を参考に循環電流を計算しましょう。
\(\dot{I}=\displaystyle\frac{V_B-V_A}{r_A+x_A+r_B+x_B}\)
\(=\displaystyle\frac{220-219.27}{0.013+j0.022+0.010+j0.020}\)
\(=\displaystyle\frac{0.73}{0.023+j0.042}\)
\(I=\displaystyle\frac{0.73}{\sqrt{0.023^2+0.042^2}}\)
\(=\displaystyle\frac{0.73}{\sqrt{0.002293}}\)
\(=15.2[A]\)
したがって、最も近い(3)が正解です。
