電験三種の過去問解説(電力):2016年(平成28)問9
三相3線式1回線の送電線路における負荷の有効電力(計算)
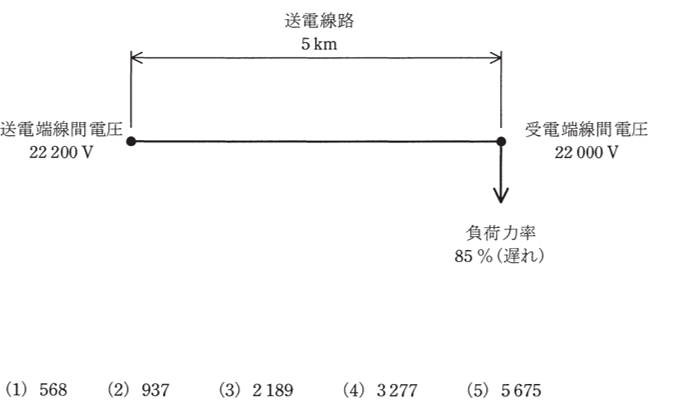
図のように、こう長5kmの三相3線式1回線の送電線路がある。この送電線路における送電端線間電圧が22200V、受電端線間電圧が22000V、負荷力率が85%(遅れ)であるとき、負荷の有効電力[kW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、1km当たりの電線1線の抵抗は0.182Ω、リアクタンスは0.355Ωとし、その他の条件はないものとする。なお、本問では、送電端線間電圧と受電端線間電圧との位相角は小さいとして得られる近似式を用いて解答すること。
スポンサーリンク
過去問のポイント
図に情報を描き込みながら丁寧に解いていきましょう。
step
1電線1線の抵抗とリアクタンス
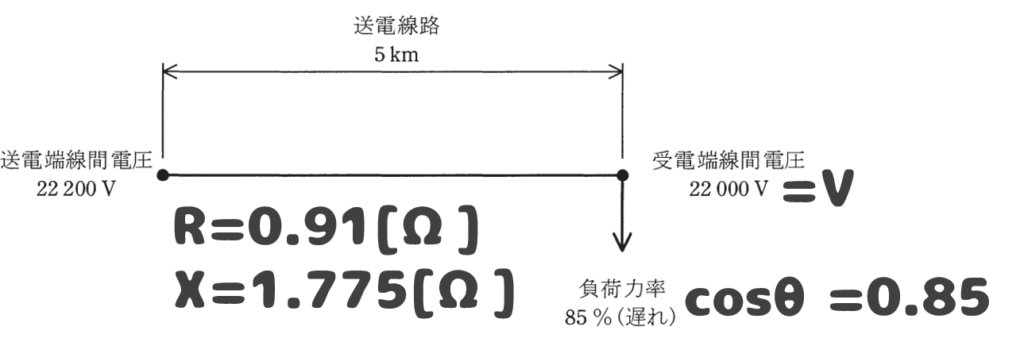
電線1線の抵抗\(R=0.182×5=0.91[Ω]\)
電線1線のリアクタンス\(X=0.355×5=1.775[Ω]\)
step
2負荷の有効電力
有効電力の公式に各値を代入しましょう
三相3線式の負荷の有効電力
\(P=\sqrt{3}VIcosθ[W]\)
ちなみに、電流\(I\)は電圧降下の公式を変形した式を代入します。
注意ポイント
\(ΔV=\sqrt{3}I(Rcosθ+Xsinθ)[V]\)
\(I=\displaystyle\frac{ΔV}{\sqrt{3}(Rcosθ+Xsinθ)}\)
\(P=\sqrt{3}V\displaystyle\frac{ΔV}{\sqrt{3}(Rcosθ+Xsinθ)}cosθ[W]\)
\(=V×\displaystyle\frac{ΔV}{Rcosθ+X\sqrt{1-cos^2θ}}cosθ[W]\)
\(=22000×\displaystyle\frac{22200-22000}{0.91×0.85+1.775×\sqrt{1-0.85^2}}×0.85\)
\(=\displaystyle\frac{3,740,000}{1.7085}\)
\(=2,189,054[W]\)
\(=2,189[kW]\)
したがって、(3)が正解です。