令和2年度(2020年):第三種電気主任技術者試験(理論)問9
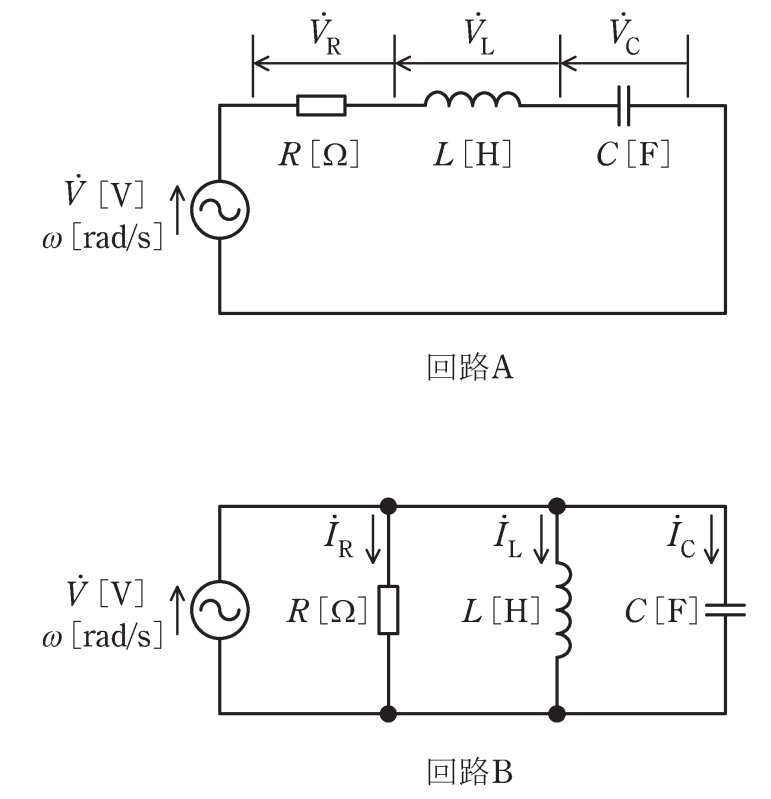
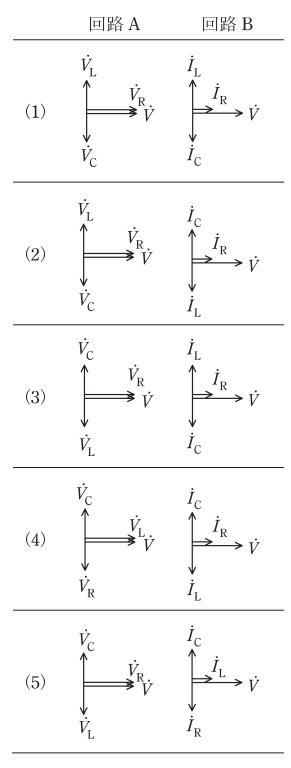
図のように、R[Ω]の抵抗、インダクタンスL[H]のコイル、静電容量C[F]のコンデンサと電圧\(\dot{V}[V]\)、角周波数ω[rad/s]の交流電源からなる二つの回路AとBがある。両回路においてそれぞれ\(ω^2LC=1\)が成り立つとき、各回路における図中の電圧ベクトルと電流ベクトルの位相の関係として、正しいものの組合せを次の(1)~(5)のうちから一つ選べ。ただし、ベクトル図における進み方向は反時計回りとする。
動画解説
過去問の解説(2020年理論問9)
この問題は、電圧ベクトルと電流ベクトルの位相関係を求める問題ですが、先ずは問題文に記載されている条件を整理しましょう。
問題文より、両回路において
\(ω^2LC=1\)
が成り立つとありますが、これは『回路Aでは直列共振条件』『回路Bでは並列共振条件』が成立していることを表しています。
step
1回路Aの電圧ベクトル
直列共振条件
インダクタンスと静電容量の端子電圧の和がゼロになる
直列共振条件より、回路Aの電験電圧は下記式で表されます
\(\dot{V}=\dot{V}_R+\dot{V}_L+\dot{V}_C\)
\(=\dot{V}_R\)
従って、電源電圧と抵抗端子の電圧ベクトルは同位相→→なので、(4)は誤りとなります。
次にインダクタンスの端子電圧は、
\(\dot{V}_L=jωL\dot{I}\)
となり、90°進み↑となる。
また、静電容量の端子電圧は、
\(\dot{V}_C=\displaystyle\frac{\dot{I}}{jωC}\)
\(=-j\displaystyle\frac{\dot{I}}{ωC}\)
となり、90°遅れ↓となるので、(3)と(5)は誤りとなります。
step
2回路Bのベクトル
並列共振条件
インダクタンスと静電容量を流れる電流の和がゼロになる
並列共振条件より、回路を流れる電流は下記式で表されます。
\(\dot{I}=\dot{I}_R+\dot{I}_L+\dot{I}_C\)
\(=\dot{I}_R\)
さらに、抵抗を流れる電流は下記のように表せるので、
\(\dot{I}_R=\displaystyle\frac{\dot{V}}{R}\)
従って、抵抗を流れる電流ベクトルと電源電圧ベクトルは同位相→→となります。
次に、インダクタンスを流れる電流は、
\(\dot{I}_L=\displaystyle\frac{\dot{V}}{jωL}\)
\(=-j\displaystyle\frac{\dot{V}}{ωL}\)
となり、90°遅れ↓となる。
また、静電容量を流れる電流は、
\(\dot{I}_C=jωC\dot{V}\)
となり、90°進み↑となるので、(2)が正解です。