電験三種の過去問解説(理論):2019年(令和元年)問4
環状鉄心の透磁率(計算)
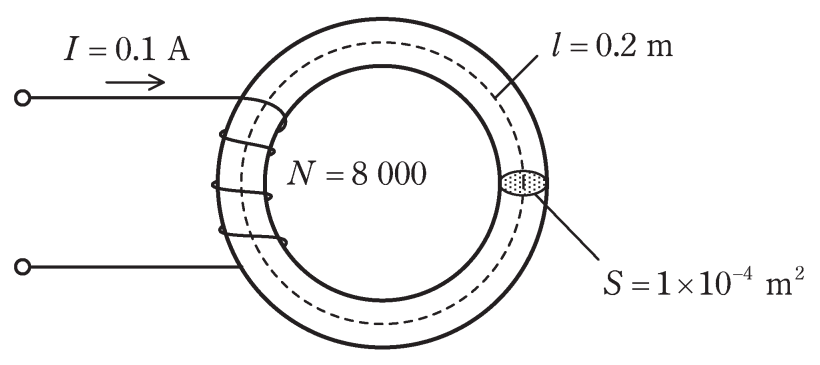
図のように、磁路の長さ ℓ=0.2m、断面積 S=1×10-4
m2 の環状鉄心に巻数 N=8000 の銅線を巻いたコイルがあ る。このコイルには直流電流 I=0.1A を流したとき、 鉄心中の磁束密度は B=1.28T であった。 このときの鉄心の透磁率μの値[H/m]として、 最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、コイルによって作られる磁束は、鉄心中を一様に通り、鉄心の外部 に漏れないものとする。
(1)\(1.6×10^{-4}\) (2)\(2.0×10^{-4}\) (3)\(2.4×10^{-4}\) (4)\(2.8×10^{-4}\) (5)\(3.2×10^{-4}\)
スポンサーリンク
過去問解説
鉄心の透磁率μを求める問題なので、下記式を覚えていた方は一瞬で解けるサービス問題です。
透磁率の式
\(μ=\displaystyle\frac{Bℓ}{NI}[H/m]\)
とは言っても、式の導出過程の中に覚えておくべき式があったりするので、導出する所から解いていきます。
透磁率μの式は、磁束Φ[Wb]の式から導出できます。
磁束Φを起磁力Fと磁気抵抗Rから求める場合
\(Φ=\displaystyle\frac{F}{R}\)
磁束Φを磁束密度Bと断面積Sから求める場合
\(Φ=BS\)
上記2式をまとめると、
\(\displaystyle\frac{F}{R}=BS\)
と表せます。
ここで、
ポイント
・起磁力\(F=NI\)
・磁気抵抗\(R=\displaystyle\frac{ℓ}{μS}\)
の関係を代入しましょう。
\(\displaystyle\frac{F}{R}=BS\)
\(\displaystyle\frac{NI}{\displaystyle\frac{ℓ}{μS}}=BS\)
\(\displaystyle\frac{μSNI}{ℓ}=BS\)
\(μ=BS×\displaystyle\frac{ℓ}{SNI}\)
\(=\displaystyle\frac{Bℓ}{NI}\)
\(=\displaystyle\frac{1.28×0.2}{8000×0.1}\)
\(=3.2×10^{-4}\)
したがって、(5)が正解です。