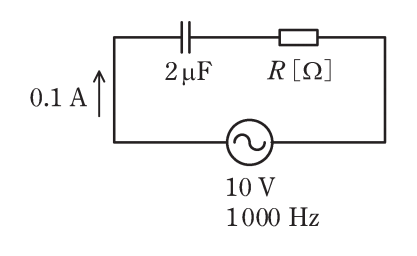
令和2年度(2020年):第三種電気主任技術者試験(理論)問8
図のように、静電容量2μFのコンデンサ、R[Ω]の抵抗を直列に接続した。この回路に、正弦波交流電圧10V、周波数1000Hzを加えたところ、電流0.1Aが流れた。抵抗Rの値[Ω]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)4.50 (2)20.4 (3)30.3 (4)60.5 (5)79.6
動画解説
過去問の解説(2020年理論問8)
まずは、RC直列交流回路の合成インピーダンスの大きさを式で表してみましょう。
合成インピーダンスは下記式で表すことができるので、
\(\dot{Z}=R+j(-\displaystyle\frac{1}{ωC})\)
合成インピーダンスの大きさは
\(|\dot{Z}|=\sqrt{R^2+(-\displaystyle\frac{1}{ωC})^2}\)
となります。
このとき、角周波数ωは
\(ω=2πf\)
と表せるので、
①式
\(|\dot{Z}|=\sqrt{R^2+(-\displaystyle\frac{1}{2πfC})^2}\)
となります。
①式を、Rを求める形に変換すると、
\(|\dot{Z}|^2=R^2+(-\displaystyle\frac{1}{2πfC})^2\)
\(R=\sqrt{|\dot{Z}|^2-(-\displaystyle\frac{1}{2πfC})^2}\)
となります。
さらに、合成インピーダンスは電圧÷電流で表されるので、
\(R=\sqrt{(\displaystyle\frac{|\dot{E}|}{|\dot{I}|})^2-(-\displaystyle\frac{1}{2πfC})^2}\)
ここで、各値を代入すると、
\(R=\sqrt{(\displaystyle\frac{10}{0.1})^2-(-\displaystyle\frac{1}{2×3.14×1000×2×10^{-6}})^2}\)
\(=\sqrt{100^2-(-79.6)^2}\)
\(=60.5\)
よって、(4)が正解です。