電験三種/電力/過去問解説:2019年(令和元年)問17
三相3線式配電線路の電力損失と増設できる負荷電力(計算)
三相3線式配電線路の受電端に遅れ力率0.8の三相平衡負荷60kW(一定)が接続されている。次の(a)及び(b)の問に答えよ。
ただし、三相負荷の受電端電圧は6.6kV一定とし、配電線路のこう長は2.5km、電線1線当たりの抵抗は0.5Ω/km、リアクタンスは0.2Ω/kmとする。なお、送電端電圧と受電端電圧の位相角は十分小さいものとして得られる近似式を用いて解答すること。また、配電線路こう長が短いことから、静電容量は無視できるものとする。(a)この配電線路での抵抗による電力損失の値[W]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)22 (2)54 (3)65 (4)161 (5)220 (b)受電端の電圧降下率が2.0%以内にする場合、受電端でさらに増設できる負荷電力(最大)の値[kW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、負荷の力率(遅れ)は変わらないものとする。
(1)476 (2)536 (3)546 (4)1280 (5)1340
スポンサーリンク
過去問の解説
公式を覚えていれば簡単な計算問題ですが、問題文を良く読まないと、代入する数値を間違えてしまう引っかけ問題ですね。
今回正解した方も、試験本番では緊張感からの焦りがあるので、問題文をよく読むことをオススメします。
(a):配電線路での抵抗による電力損失
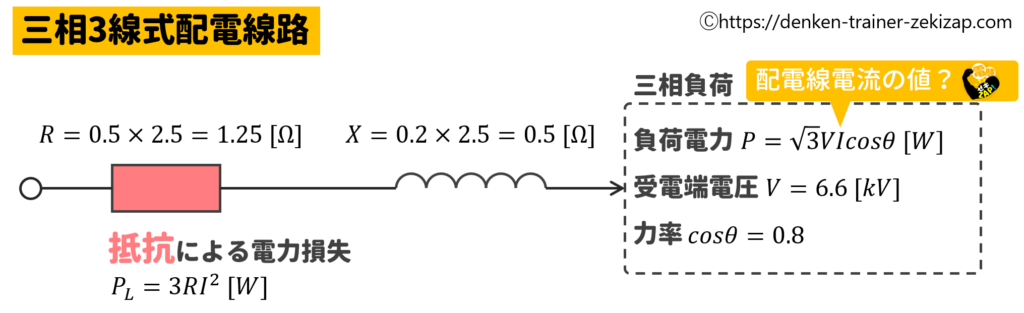
電力損失の公式
\(P_L=3RI^2[W]\)
抵抗Rは1.25[Ω]ですが、配電線電流\(I[A]\)を求める必要があります。
三相負荷電力の公式を利用しましょう。
\(P=\sqrt3VIcosθ\)
\(I=\displaystyle\frac{P}{\sqrt3Vcosθ}\)
\(=\displaystyle\frac{60×10^3}{\sqrt3×6.6×10^3×0.8}\)
\(=\displaystyle\frac{60}{\sqrt3×6.6×0.8}\)
\(=6.56[A]\)
電力損失の公式に求めた配電線電流6.56[A]と抵抗1.25[Ω]を代入しましょう
\(P_L=3RI^2\)
\(=3×1.25×6.56^2\)
\(=161[W]\)
したがって、(4)が正解です。
スポンサーリンク
(b):受電端の電圧降下率2.0%以内で増設できる負荷電力
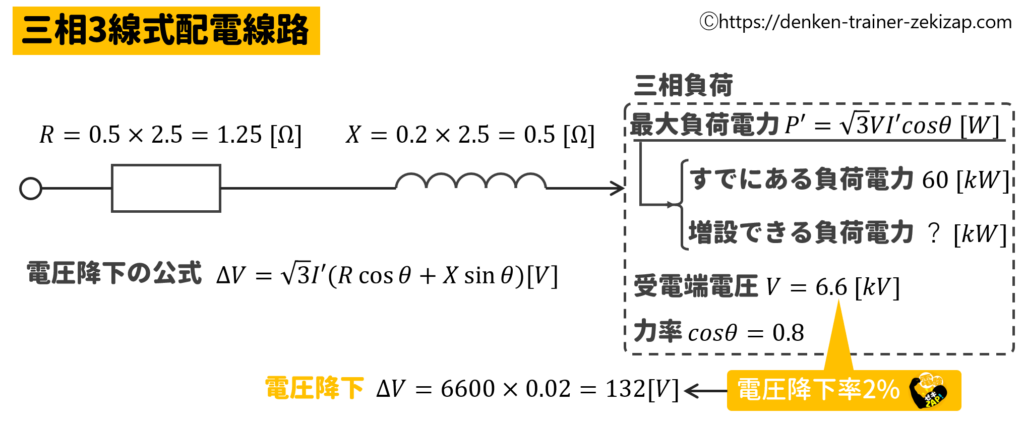
電圧降下率2%となる電圧降下の値\(ΔV\)は次のように求められます。
\(ΔV=6.6×10^3×0.02=132[V]\)
今回は求める増設できる負荷電力は、『最大負荷電力-すでにある負荷電力』で求められます。
最大負荷電力\(P'\)を求めるには、最大電流\(I'\)を求める必要があります。
最大電流\(I'\)は電圧降下\(ΔV\)の公式から求められます。
\(ΔV=\sqrt3I'(Rcosθ+Xsinθ)\)
\(I'=\displaystyle\frac{ΔV}{\sqrt3(Rcosθ+Xsinθ)}\)
\(=\displaystyle\frac{132}{\sqrt3(1.25×0.8+0.5×0.6)}\)
\(=58.62[A]\)
最大負荷電力の公式に各値を代入しましょう。
\(P'=\sqrt3VI'cosθ\)
\(=\sqrt3×6.6×10^3×58.62×0.8\)
\(=536[kW]\)
ここで計算をやめないで下さい!!
ここまでで求めたのは、最大負荷電力です。
今回求めるのは、増設できる負荷電力なので、最大負荷電力からすでにある負荷電力を引き算して下さい。
\(536-60=476[kW]\)
したがって、(1)が正解です。
