電験三種の過去問解説(電力):2019年(令和元年)問16
受電端の線間電圧と1線当たりの送電端電流(計算)
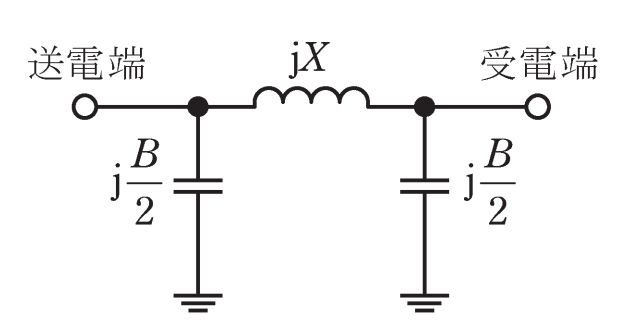
送電線のフェランチ現象に関する問である。三相3線式1回線送電線の一相が図のπ形等価回路で表され、送電線路のインピーダンス\(jX=j200Ω\)、アドミタンス\(jB=j0.800mS\)とし、送電端の線間電圧が\(66.0kV\)であり、受電端が無負荷のとき、次の(a)及び(b)の問に答えよ。
(a)受電端の線間電圧の値[kV]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)66.0 (2)71.7 (3)78.6 (4)114 (5)132 (b)1線当たりの送電端電流の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)15.2 (2)16.6 (3)28.7 (4)31.8 (5)55.1
スポンサーリンク
過去問の解説
初見の方の中には、解き方すら思い浮かばない…そんな感じの問題かもしれませんね。
しかし、計算パターンは決まっているので、まずは解き方を覚えてしまった方が良いかもしれません。
(a)受電端の線間電圧
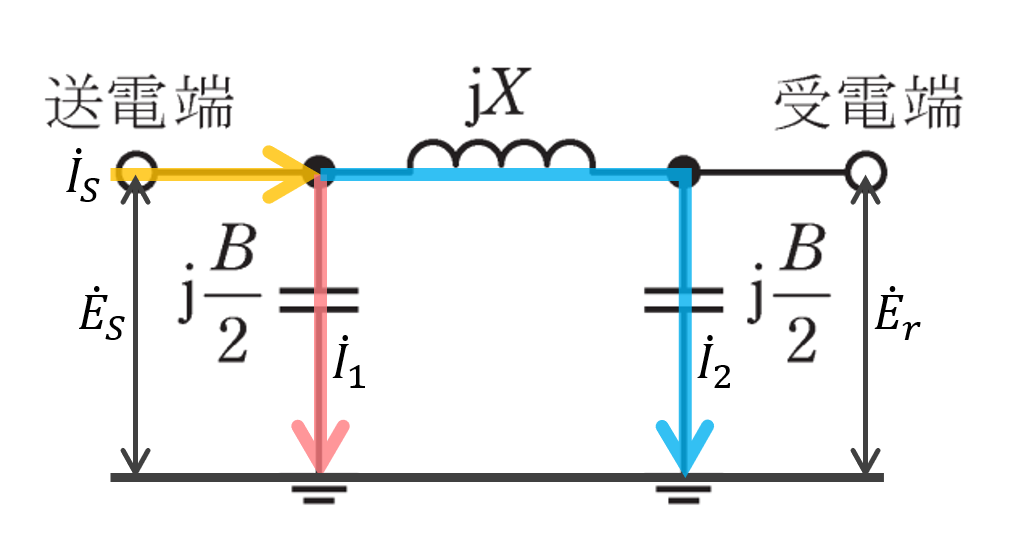
相電圧と電流は上図のように書くことができます。
問題文より、送電端の線間電圧は66kVなので、送電端の相電圧\(\dot{E_S}\)は
\(\dot{E_S}=\displaystyle\frac{66}{\sqrt3}[kV]\)
受電端は開放されているので、\(\dot{I_2}\)は
\(\dot{I_2}=j\displaystyle\frac{0.8×10^{-3}}{2}×\dot{E_r}\)
\(=j0.4×10^{-3}×\dot{E_r}\)
と表せるので、送電端の相電圧\(\dot{E_S}\)と電流\(\dot{I_2}\)の関係から
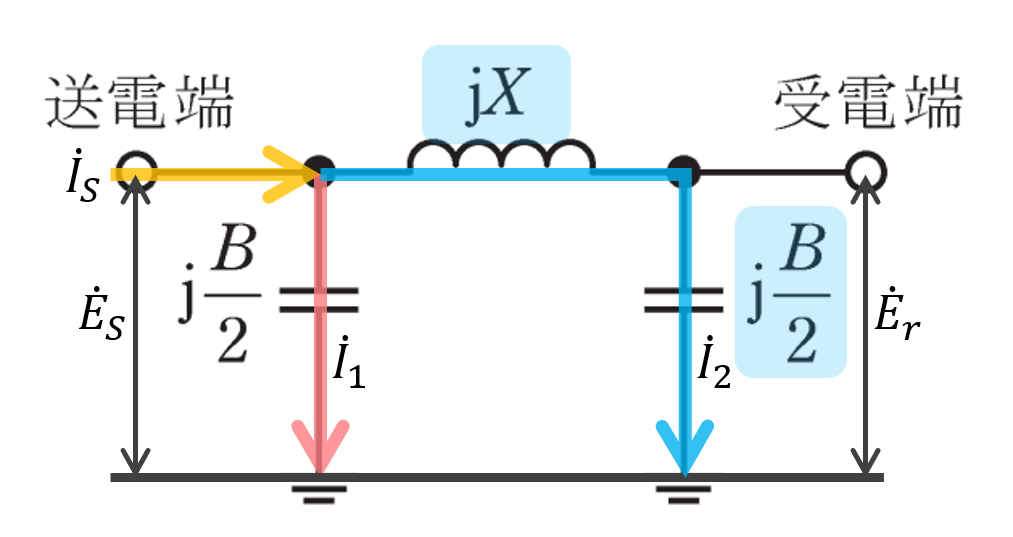
\(\dot{E_S}=jX\dot{I_2}+\dot{E_r}\)
\(\dot{E_S}=j200×j0.4×10^{-3}×\dot{E_r}+\dot{E_r}\)
\(\dot{E_S}=-0.08\dot{E_r}+\dot{E_r}\)
\(\dot{E_S}=0.92\dot{E_r}\)
\(\dot{E_r}=\displaystyle\frac{\dot{E_S}}{0.92}\)
\(\dot{E_r}=\displaystyle\frac{\displaystyle\frac{66}{\sqrt3}}{0.92}\)
\(\dot{E_r}=41.42[kV]\)
ここまでの計算で求めたのは、受電端の相電圧です。
求めたいのは、受電端の線間電圧なので相電圧に\(\sqrt3\)をかけましょう♪
\(41.42×\sqrt3=71.7[kV]\)
したがって、(2)が正解です。
(b)1線当たりの送電端電流
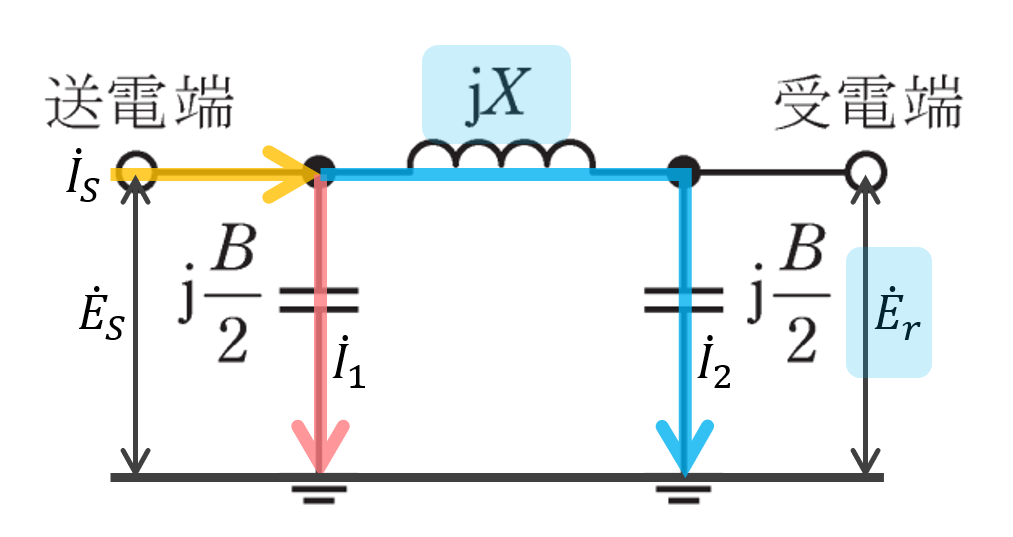
(a)で受電端の相電圧\(\dot{E_r}=41.42[kV]\)が求められたので、電流\(\dot{I_2}\)は
\(\dot{I_2}=j0.4×10^{-3}×\dot{E_r}\)
\(=j0.4×10^{-3}×41.42×10^{3}\)
\(=j16.57[A]\)
一方、電流\(\dot{I_1}\)は
\(\dot{I_1}=j0.4×10^{-3}×\dot{E_s}\)
\(=j0.4×10^{-3}×\displaystyle\frac{66×10^3}{\sqrt3}\)
\(=j15.24[A]\)
図を見てわかる通り、1線当たりの送電端電流は電流\(\dot{I_1}\)と\(\dot{I_2}\)の合計なので、
\(\dot{I_S}=\dot{I_1}+\dot{I_2}\)
\(=j15.24+j16.57\)
\(=j31.8[A]\)
つまり、\(I_S=31.8[A]\)となるため、(4)が正解です。