【ヒント掲載で使い易い】電験三種(電力)の過去問題集2019★動画と図でやさしく解説

電験三種の過去問解説(電力)：2019年(令和元年)問13
支線の張力は電線の張力の何倍か(計算)

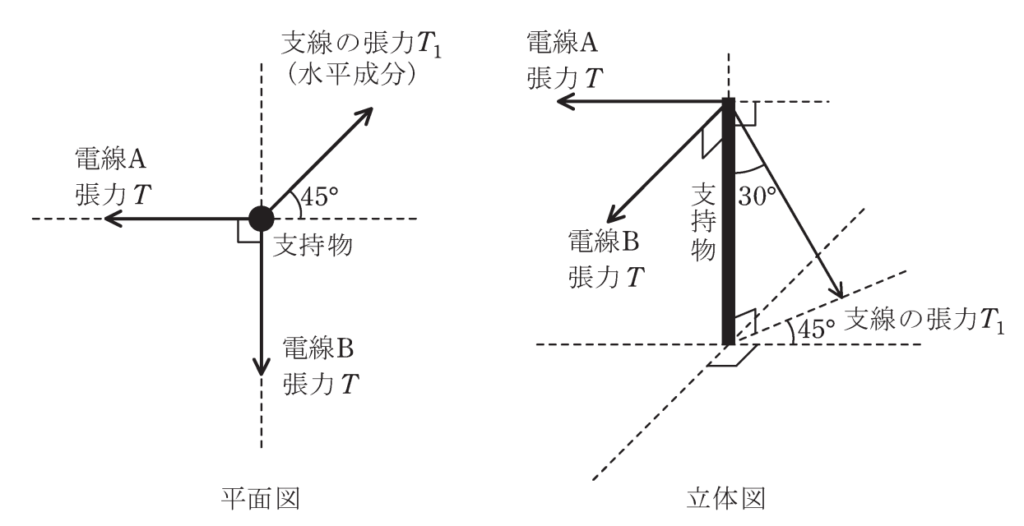
図に示すように、電線A,Bの張力を、支持物を介して支線で受けている。電線A,Bの張力の大きさは等しく、その値をTとする。支線に加わる張力T1は電線張力Tの何倍か。最も近いものを次の(1)～(5)のうちから一つ選べ。

なお、支持物は地面に垂直に立てられており、各電線は支線の取付け高さと同じ高さに取り付けられている。また、電線A,Bは地面に水平に張られているものとし、電線A,B及び支線の自重は無視する。

(1)\(\displaystyle\frac{1}{2}\)

(2)\(\displaystyle\frac{\sqrt2}{2}\)

(3)\(\sqrt2\)

(4)\(2\)

(5)\(2\sqrt2\)

出典元：一般財団法人電気技術者試験センター

スポンサーリンク

過去問の解説

step
1電線Aと電線Bの合成張力

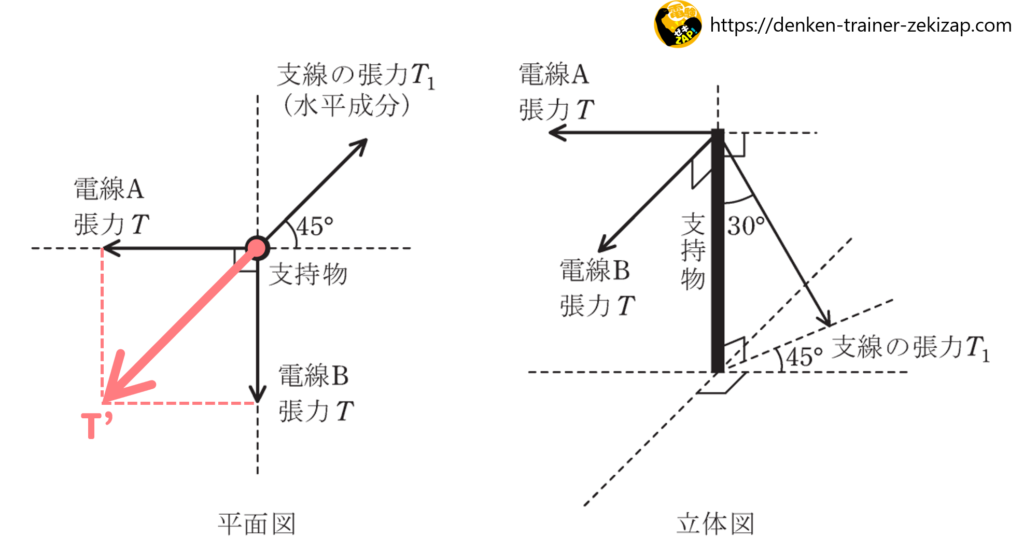
電線Aと電線Bは同一平面上で異なる方向に同じ大きさの張力が生じています。

つまり、45°の直角三角形の三角比の関係が成り立ちます。

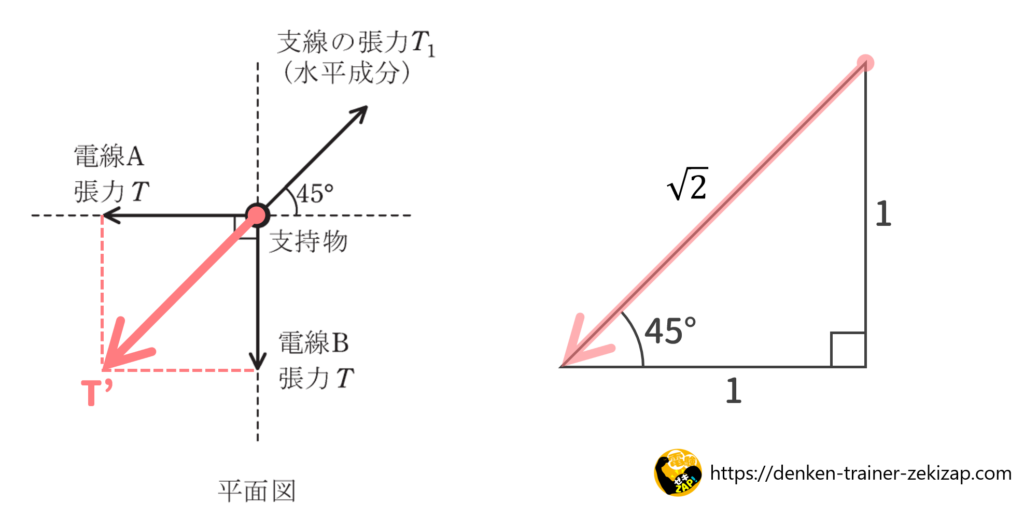
\(1:\sqrt2=T:T'\)

　　\(T'=\sqrt2T\)

step
2支線張力の水平成分

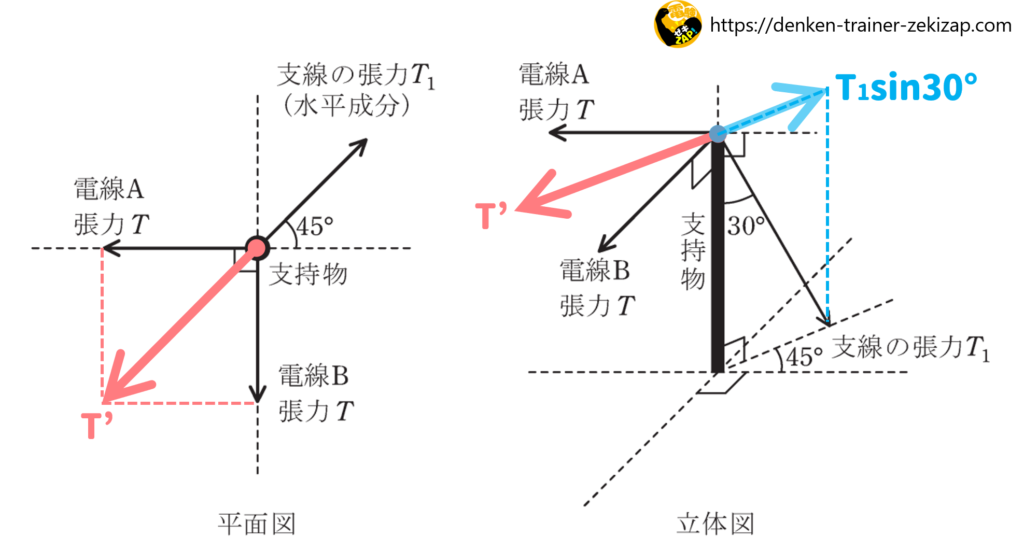
続いて、支線張力の水平成分は\(T_1sin30°\)で表されるので、

\(T_1sin30°=\displaystyle\frac{T_1}{2}\)

step
3支線に加わる張力T1は電線張力Tの何倍か

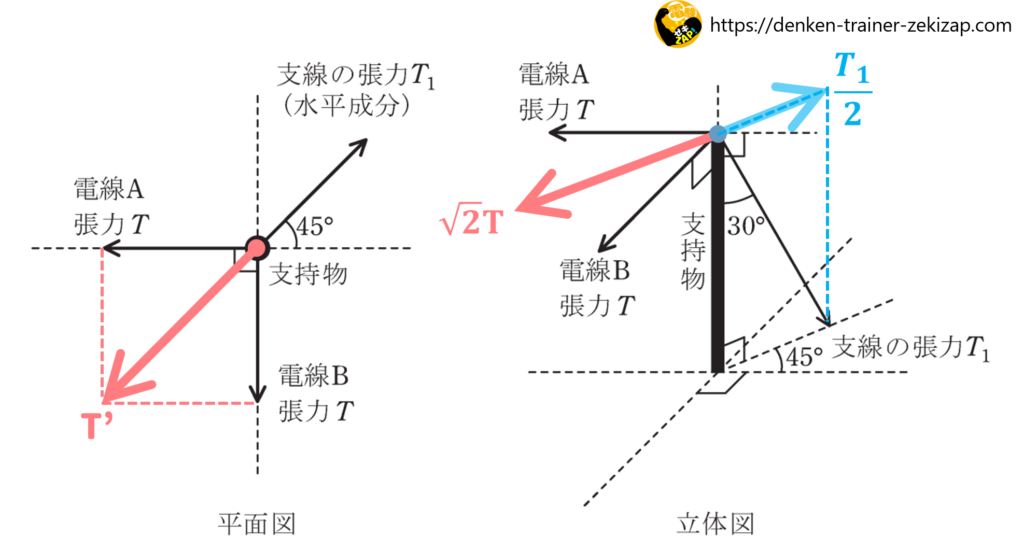
電線の合成張力と支線張力の水平成分は等しいので、

\(\displaystyle\frac{T_1}{2}=\sqrt2T\)

\(\displaystyle\frac{T_1}{T}=2\sqrt2\)

したがって、(5)が正解です。