電験三種の過去問解説(電力):2019年(令和元年)問8
過電流継電器の動作時間(計算)
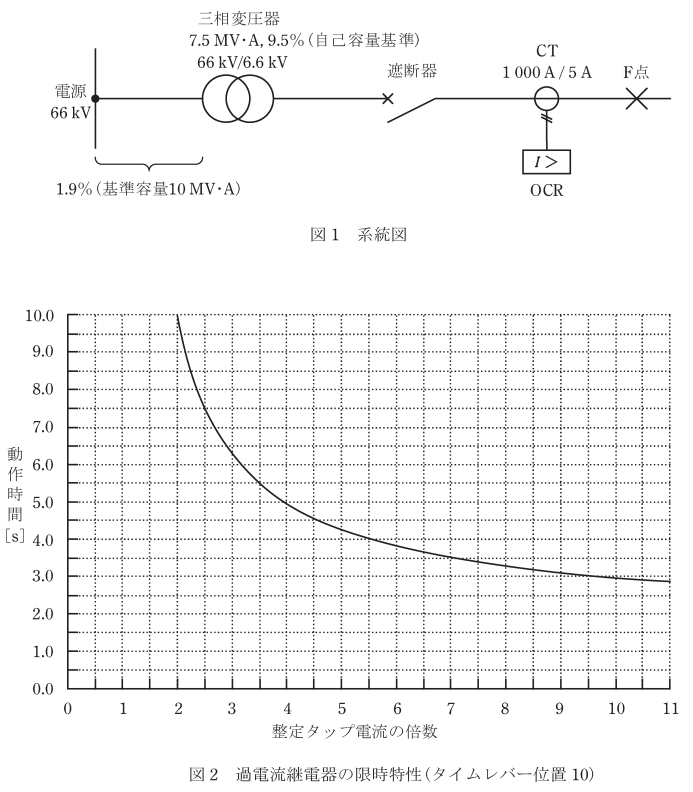
図1のように、定格電圧66kVの電源から三相変圧器を介して二次側に遮断器が接続された三相平衡系統がある。三相変圧器は定格容量7.5MV・A、変圧比66kV/6.6kV、百分率インピーダンスが自己容量基準で9.5%である。また、三相変圧器一次側から電源側をみた百分率インピーダンスは基準容量10MV・Aで1.9%である。過電流継電器(OCR)は変流比1,000A/5Aの計器用変流器(CT)の二次側に接続されており、整定タップ電流値5A、タイムレバー位置1に整定されている。図1のF点で三相短絡事故が発生したとき、過電流継電器の動作時間[s]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、三相変圧器二次側からF点までのインピーダンス及び負荷は無視する。また、過電流継電器の動作時間は図2の限流特性に従い、計器用変流器の磁気飽和は考慮しないものとする。
(1)0.29 (2)0.34 (3)0.38 (4)0.46 (5)0.56
スポンサーリンク
過去問の解説
step
1合成パーセントインピーダンス
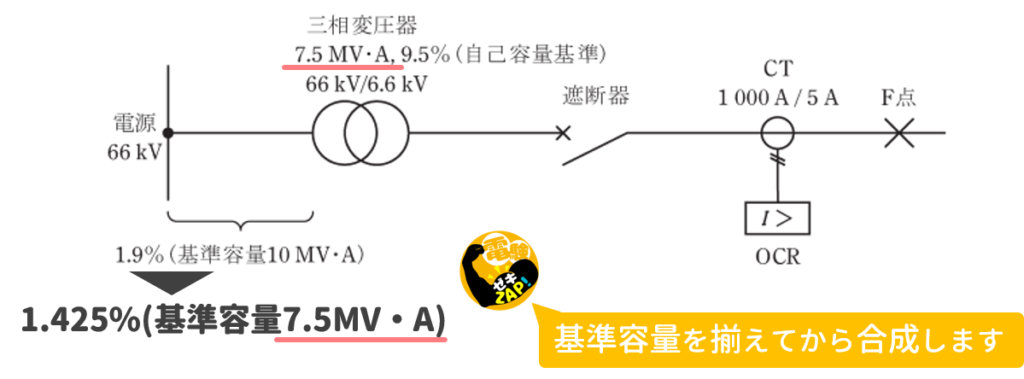
三相変圧器の容量が定格容量7.5MV・Aで9.5%、三相変圧器から電源側が基準容量10MV・Aで1.9%です。
それぞれを足し算して、合成パーセントインピーダンスを求めますが、基準容量が異なるため、単純に足し算することができません。
そこで、三相変圧器から電源側が基準容量を10MV・Aから7.5MV・Aにした場合のパーセントインピーダンスを求めて、足し算しましょう。
\(10:7.5=1.9:x\)
\(10x=7.5×1.9\)
\(x=1.425[\%]\)
三相変圧器から電源側の基準容量を7.5MV・Aとした場合のパーセントインピーダンスが求められたので、合成パーセントインピーダンスを求めましょう。
\(\%Z=1.425+9.5=10.925[\%]\)
step
2変圧器2次側の定格電流
変圧器容量の式
\(P=\sqrt3V_{n2}I_{n2}[V・A]\)
式を変換して変圧器二次側の定格電流\(I_{n2}\)を求めましょう。
\(I_{n2}=\displaystyle\frac{P}{\sqrt3V_{n2}}\)
\(I_{n2}=\displaystyle\frac{7.5×10^6}{\sqrt3×6.6×10^3}\)
\(I_{n2}=656.08[A]\)
step
3変圧器二次側の短絡電流
パーセントインピーダンスの公式
\(\%Z=\displaystyle\frac{I_{n2}}{I_{S2}}×100[\%]\)
式を変換して変圧器二次側の短絡電流\(I_{S2}\)を求めましょう。
\(I_{S2}=\displaystyle\frac{I_{n2}}{\%Z}×100\)
\(I_{S2}=\displaystyle\frac{656.08}{10.925}×100\)
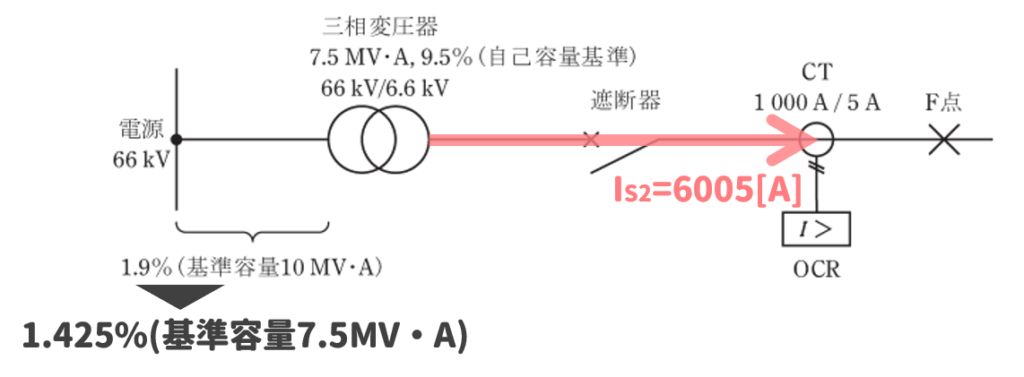
\(I_{S2}=6005[A]\)
step
4変流器二次側の電流
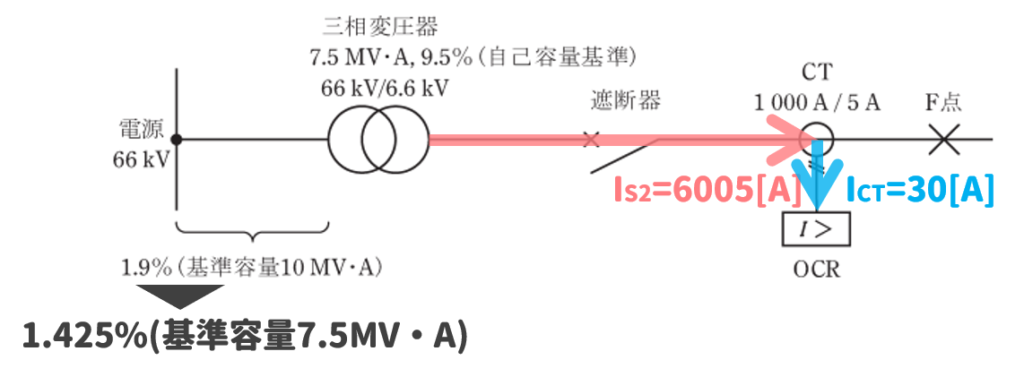
続いて、変流器2次側の電流\(I_{CT}\)を変流比1000A/5Aの関係から求めましょう。
\(1000:5=6005:I_{CT}\)
\(1000×I_{CT}=5×6005\)
\(I_{CT}=30.025[A]\)
step
5過電流継電器の動作時間
変流器2次側の電流\(I_{CT}\)が整定タップ電流値5Aの何倍か求めましょう。
整定タップ電流の倍数\(=\displaystyle\frac{30.025}{5}=6\)
整定タップ電流の倍数が6なので、グラフより、
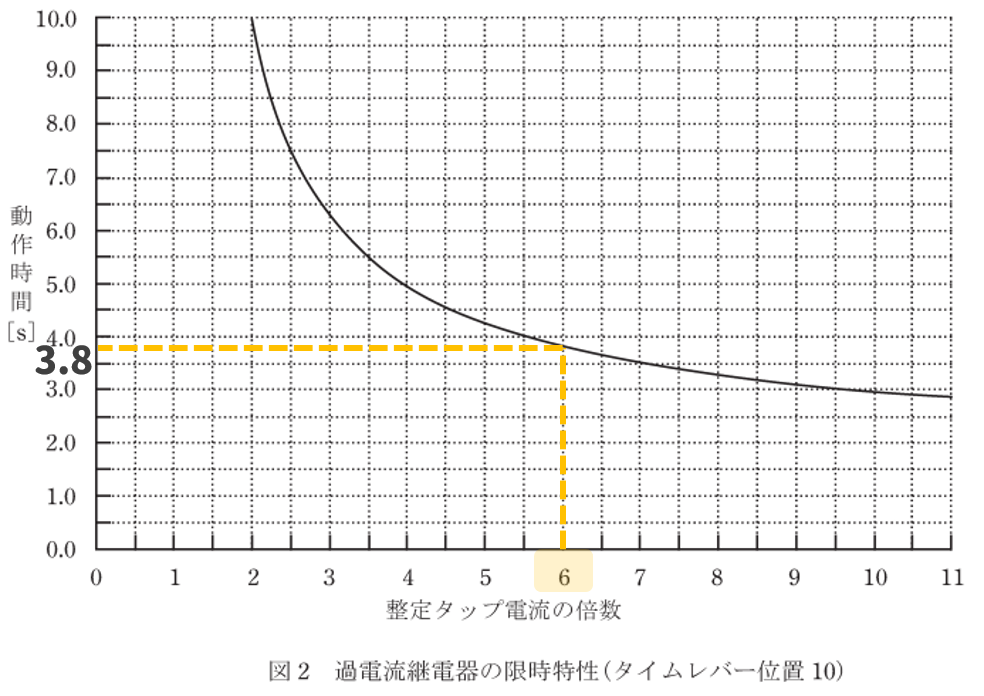
動作時間は3.8[s]となるが、グラフの限時特性はタイムレバー位置10の場合である。
今回求めるのは、タイムレバー位置1の場合での動作時間なので、
動作時間\(=\displaystyle\frac{3.8}{10}=0.38[s]\)
したがって、(3)が正解です。